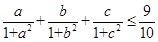题目内容
(本题满分16分)设
(1)请写出 的表达式(不需证明);
的表达式(不需证明);
(2)求 的极值
的极值
(3)设 的最大值为
的最大值为 ,
, 的最小值为
的最小值为 ,求
,求 的最小值.
的最小值.

(1)请写出
 的表达式(不需证明);
的表达式(不需证明);(2)求
 的极值
的极值(3)设
 的最大值为
的最大值为 ,
, 的最小值为
的最小值为 ,求
,求 的最小值.
的最小值.(1)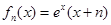 ;
;
(2) 的极小值为
的极小值为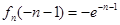 ;
;
(3)当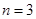 时,
时, 取得最小值
取得最小值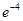
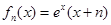 ;
;(2)
 的极小值为
的极小值为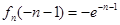 ;
;(3)当
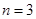 时,
时, 取得最小值
取得最小值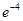
(1)分别列出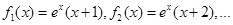 可归纳出
可归纳出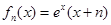 .
.
(2)因为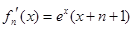 ,然后令
,然后令 ,然后再根据极大(小)值的判断方法可求出
,然后再根据极大(小)值的判断方法可求出 存在极小值,无极大值.
存在极小值,无极大值.
(3)根据二次函数的最值研究方法可得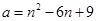 ,
,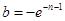 ,
,
从而可得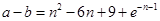 ,
,
然后再令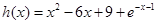 ,然后利用导数研究其单调性可知a-b在n=3时取得最小值.
,然后利用导数研究其单调性可知a-b在n=3时取得最小值.
(1)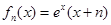 ……………………………4分
……………………………4分
(2)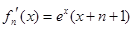
 …………………………………5分
…………………………………5分
…………7分
所以 的极小值为
的极小值为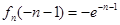 …………8分
…………8分
(3)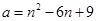
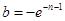
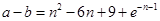 ………………………………10分
………………………………10分
令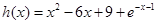
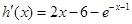 在R上递增
在R上递增
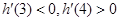
令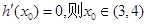
且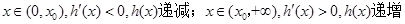
所以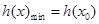 ………………………………14分
………………………………14分
所以当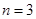 时,
时, 取得最小值
取得最小值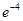 ……………………16分
……………………16分
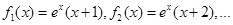 可归纳出
可归纳出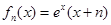 .
.(2)因为
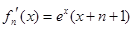 ,然后令
,然后令 ,然后再根据极大(小)值的判断方法可求出
,然后再根据极大(小)值的判断方法可求出 存在极小值,无极大值.
存在极小值,无极大值.(3)根据二次函数的最值研究方法可得
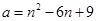 ,
,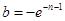 ,
,从而可得
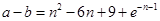 ,
,然后再令
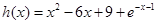 ,然后利用导数研究其单调性可知a-b在n=3时取得最小值.
,然后利用导数研究其单调性可知a-b在n=3时取得最小值.(1)
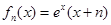 ……………………………4分
……………………………4分(2)
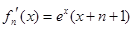
 …………………………………5分
…………………………………5分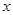 | 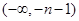 | 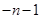 | 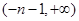 |
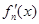 | -- | 0 | + |
 | 减 | 极小值 | 增 |
所以
 的极小值为
的极小值为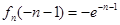 …………8分
…………8分(3)
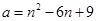
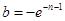
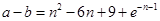 ………………………………10分
………………………………10分令
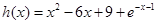
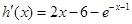 在R上递增
在R上递增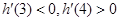
令
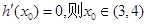
且
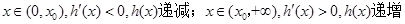
所以
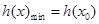 ………………………………14分
………………………………14分所以当
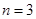 时,
时, 取得最小值
取得最小值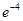 ……………………16分
……………………16分
练习册系列答案
相关题目
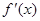 为f(x)的导函数,求证:
为f(x)的导函数,求证: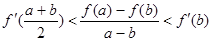
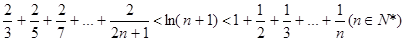
 ,
,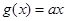 ,
,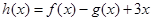 ,其中
,其中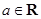 且
且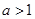 .
.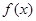 的导函数
的导函数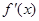 的最小值;
的最小值;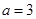 时,求函数
时,求函数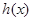 的单调区间及极值;
的单调区间及极值;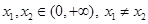 ,函数
,函数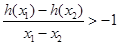 ,求实数
,求实数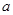 的取值范围.
的取值范围. 的导函数
的导函数 的图象大致是( )
的图象大致是( )
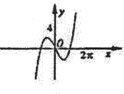


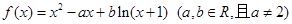
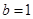 且函数
且函数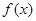 在其定义域上为增函数时,求
在其定义域上为增函数时,求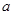 的取值范围;
的取值范围;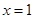 处取得极值,试用
处取得极值,试用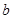 ;
;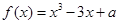 有3个不同的零点,则实数
有3个不同的零点,则实数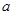 的取值范围是( )
的取值范围是( )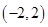
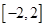
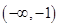
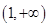
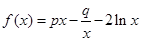 ,且
,且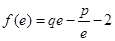 ,其中
,其中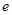 是自然对数的底数.
是自然对数的底数.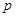 与
与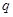 的关系;
的关系;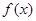 在其定义域内为单调函数,求
在其定义域内为单调函数,求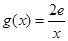 ,若在
,若在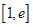 上至少存在一点
上至少存在一点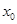 ,使得
,使得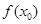 >
> 成立,求实数
成立,求实数
 在
在 上为增函数,求实数
上为增函数,求实数 的取值范围;
的取值范围; 时,求
时,求 上的最大值和最小值;
上的最大值和最小值; ,
, 恒成立.
恒成立. 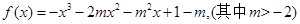 的图像在
的图像在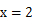 处的切线与直线
处的切线与直线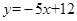 平行。
平行。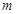 的直线;
的直线;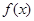 在区间
在区间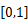 上的最小值;
上的最小值;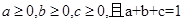 ,利用结论(2)证明:
,利用结论(2)证明: