题目内容
.(本小题满分12分)
已知函數f(x)=ln+mx2(m∈R)
(I)求函数f(x)的单调区间;
(II)若m=0,A(a,f(a))、B(b,f(b))是函数f(x)图象上不同的两点,且a>b>0,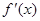 为f(x)的导函数,求证:
为f(x)的导函数,求证: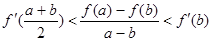
(III)求证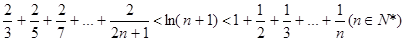
已知函數f(x)=ln+mx2(m∈R)
(I)求函数f(x)的单调区间;
(II)若m=0,A(a,f(a))、B(b,f(b))是函数f(x)图象上不同的两点,且a>b>0,
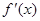 为f(x)的导函数,求证:
为f(x)的导函数,求证: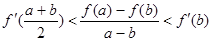
(III)求证
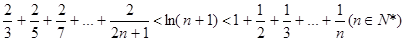
(1) 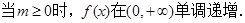
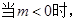
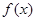 在
在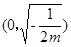 上单调递增,在
上单调递增,在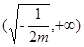 上单调递减.
上单调递减.
(2)构造函数利用单调性来证明不等式成立。
(3)在第二问的基础上,进行适当的放缩得到证明。
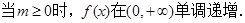
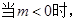
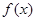 在
在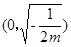 上单调递增,在
上单调递增,在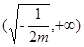 上单调递减.
上单调递减. (2)构造函数利用单调性来证明不等式成立。
(3)在第二问的基础上,进行适当的放缩得到证明。
试题分析:解:(Ⅰ)f(x)的定义域为
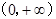 ,
, 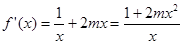
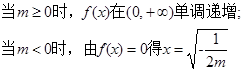
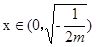 时,
时,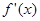 >0,
>0, 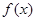 在
在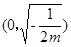 上单调递增;
上单调递增;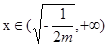 时,
时,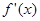 <0,
<0, 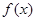 在
在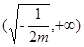 上单调递减.
上单调递减.综上所述:
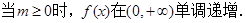
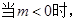
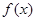 在
在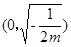 上单调递增,在
上单调递增,在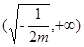 上单调递减.…………3分
上单调递减.…………3分(Ⅱ)要证
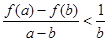 ,只需证
,只需证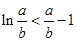 ,令
,令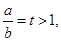 即证
即证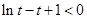 ,
,令
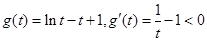 ,
,因此
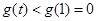 得证.…………………6分
得证.…………………6分要证
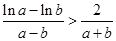 ,只要证
,只要证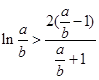 ,
,令
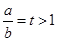 ,只要证
,只要证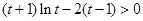 ,
,令
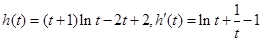 ,
,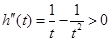 因此
因此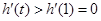 ,
,所以
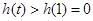 得证.………………9分
得证.………………9分另一种的解法:
令
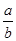 =
=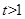 ,
,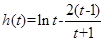 ,
,则
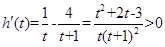
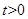 ,
,所以
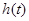 在
在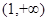 单调递增,
单调递增,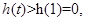
即
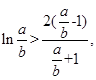 得证.
得证.(Ⅲ)由(Ⅱ)知
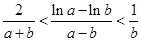 ,(
,(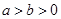 ),则
),则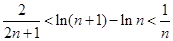
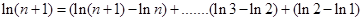
所以
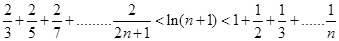 .………………12分
.………………12分点评:解决该试题的关键是利用导数的正负来求解函数的单调区间,进而确定出最值,同时利用构造函数的思想,分离参数来求解函数的最值,解决不等式的恒成立问题,同时要对于不等式的证明,要采用适当的放缩来完成,属于难度试题。

练习册系列答案
相关题目
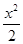 -aln(x+1),a∈R.
-aln(x+1),a∈R. 在(1,4)上是减函数,则实数
在(1,4)上是减函数,则实数 的取值范围是( )
的取值范围是( )



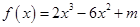 (
(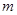 为常数)在
为常数)在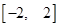 上有最大值3,那么此函数在
上有最大值3,那么此函数在
 ,求
,求 的单调区间;
的单调区间; ≥0时
≥0时 的取值范围.
的取值范围.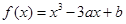 在点
在点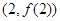 处与直线
处与直线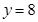 相切,则
相切,则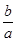 为 .
为 .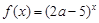 是R上的减函数;命题q:在
是R上的减函数;命题q:在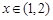 时,不等式
时,不等式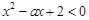 恒成立,若p∪q是真命题,求实数a的取值范围.
恒成立,若p∪q是真命题,求实数a的取值范围. 。
。 ,而使得不等式
,而使得不等式 能成立,求实数
能成立,求实数 的最小值;
的最小值; 在区间
在区间 上恰有两个不同的零点,求实数
上恰有两个不同的零点,求实数 的取值范围。
的取值范围。
 的表达式(不需证明);
的表达式(不需证明); 的最大值为
的最大值为 ,
, ,求
,求 的最小值.
的最小值.