题目内容
(本小题满分13分)已知数列{an},定义 (n∈N+)是数列{an}的倒均数. (1)若数列{an}的倒均数是
(n∈N+)是数列{an}的倒均数. (1)若数列{an}的倒均数是 ,求数列{an}的通项公式;(2)若等比数列{bn}的首项为–1,公比为q =
,求数列{an}的通项公式;(2)若等比数列{bn}的首项为–1,公比为q = ,其倒均数为Vn,问是否存在正整数m,使得当n≥m(n∈N+)时,Vn<–16恒成立?若存在,求m的最小值;若不存在,请说明理由.
,其倒均数为Vn,问是否存在正整数m,使得当n≥m(n∈N+)时,Vn<–16恒成立?若存在,求m的最小值;若不存在,请说明理由.
 (n∈N+)是数列{an}的倒均数. (1)若数列{an}的倒均数是
(n∈N+)是数列{an}的倒均数. (1)若数列{an}的倒均数是 ,求数列{an}的通项公式;(2)若等比数列{bn}的首项为–1,公比为q =
,求数列{an}的通项公式;(2)若等比数列{bn}的首项为–1,公比为q = ,其倒均数为Vn,问是否存在正整数m,使得当n≥m(n∈N+)时,Vn<–16恒成立?若存在,求m的最小值;若不存在,请说明理由.
,其倒均数为Vn,问是否存在正整数m,使得当n≥m(n∈N+)时,Vn<–16恒成立?若存在,求m的最小值;若不存在,请说明理由.(Ⅰ) 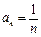 (Ⅱ) m = 7.
(Ⅱ) m = 7.
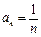 (Ⅱ) m = 7.
(Ⅱ) m = 7. (1)由 得
得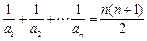 ①………1分
①………1分
当n = 1时,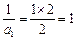 ,∴a1 = 1.……2分
,∴a1 = 1.……2分
当n≥2时,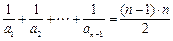 ②
②
①– ②得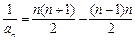 ,即
,即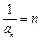 ,∴
,∴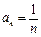 ………分
………分
(2)bn =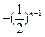 ,
,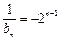
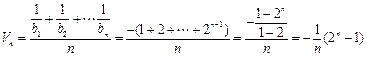 ……8分
……8分
令Vn<–16得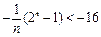 .即
.即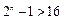 n,
n,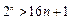 .
.
当n = 6时,26 <16×6 +1,当n = 7时,27 = 128,16×7 + 1 = 113,27>16×7 + 1.
下面证当n≥7(n∈N+)时,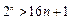 成立.…10分
成立.…10分
1°当n = 7时,已证; 2°假设当n = k时,2k>16k + 1成立,
当n = k + 1时,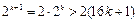 =16k + 16k + 2 >16k + 16 +1 = 16(k + 1) + 1
=16k + 16k + 2 >16k + 16 +1 = 16(k + 1) + 1
这就是说,当n = k + 1时,结论也成立.
由1°,2°可知,当n≥7时,2n>16n + 1成立.故m的最小值为m = 7.
此题也可用导数法证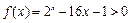 对
对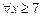 成立.………13分
成立.………13分
 得
得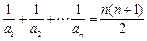 ①………1分
①………1分当n = 1时,
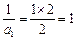 ,∴a1 = 1.……2分
,∴a1 = 1.……2分当n≥2时,
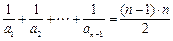 ②
②①– ②得
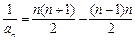 ,即
,即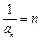 ,∴
,∴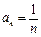 ………分
………分(2)bn =
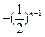 ,
,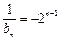
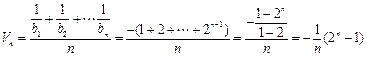 ……8分
……8分令Vn<–16得
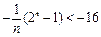 .即
.即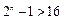 n,
n,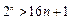 .
.当n = 6时,26 <16×6 +1,当n = 7时,27 = 128,16×7 + 1 = 113,27>16×7 + 1.
下面证当n≥7(n∈N+)时,
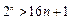 成立.…10分
成立.…10分1°当n = 7时,已证; 2°假设当n = k时,2k>16k + 1成立,
当n = k + 1时,
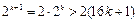 =16k + 16k + 2 >16k + 16 +1 = 16(k + 1) + 1
=16k + 16k + 2 >16k + 16 +1 = 16(k + 1) + 1这就是说,当n = k + 1时,结论也成立.
由1°,2°可知,当n≥7时,2n>16n + 1成立.故m的最小值为m = 7.
此题也可用导数法证
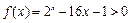 对
对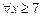 成立.………13分
成立.………13分
练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
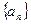 的前n项之和为Sn,令
的前n项之和为Sn,令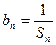 ,且
,且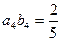 ,S6-S3=15.
,S6-S3=15.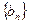 的通项公式与它的前10项之和;
的通项公式与它的前10项之和;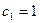 ,
,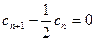 ,
,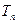 =
=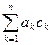 ,求
,求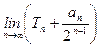 的值.
的值.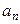 }满足
}满足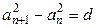 (其中d是常数,
(其中d是常数,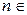 N﹡),则称数列{
N﹡),则称数列{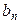 }是公差为m的差数列,则m=0是“数列{
}是公差为m的差数列,则m=0是“数列{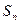 为{an}的前n项和,令bn=anan+1,数列
为{an}的前n项和,令bn=anan+1,数列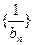 的前n项和为Tn.(1)求an和Sn;(2)求证:Tn<
的前n项和为Tn.(1)求an和Sn;(2)求证:Tn<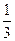 ;(3)是否存在正整数m , n ,且1<m<n ,使得T1 , Tm , Tn成等比数列?若存在,求出m ,n的值,若不存在,说明理由.
;(3)是否存在正整数m , n ,且1<m<n ,使得T1 , Tm , Tn成等比数列?若存在,求出m ,n的值,若不存在,说明理由.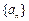 的前
的前 项和为
项和为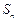 ,其中
,其中 ,
,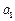 为常数,且
为常数,且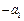 、
、 成等差数列.
成等差数列.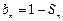 ,问:是否存在
,问:是否存在 为等比数列?若存在,求出
为等比数列?若存在,求出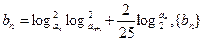 的前n项和为Tn,求
的前n项和为Tn,求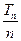 的最小值.
的最小值.