题目内容
(Ⅰ)解不等式
 .
.
(Ⅱ)设集合 ,集合
,集合 ,求
,求 ,
,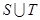 .
.
(Ⅰ)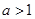 时解集为
时解集为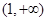 ,
,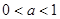 时解集为
时解集为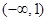 ;(2)
;(2)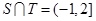 ,
,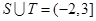 .
.
解析试题分析:(Ⅰ)先化为同底的对数不等式,再结合底数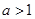 或
或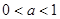 时指数函数的单调性进行分类求解;(2)先解对数不等式
时指数函数的单调性进行分类求解;(2)先解对数不等式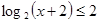 求出集合S,再求函数
求出集合S,再求函数 的值域,即集合T,最后结合集合的交、并运算求出
的值域,即集合T,最后结合集合的交、并运算求出 ,
,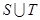 .
.
试题解析:(Ⅰ)原不等式可化为: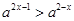 .
.
当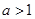 时,
时,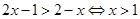 .原不等式解集为
.原不等式解集为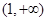 .
.
当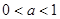 时,
时,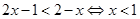 .原不等式解集为
.原不等式解集为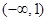 .
.
(Ⅱ)由题设得: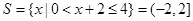 ,
,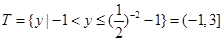 .
.
∴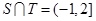 ,
,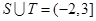 .
.
考点:指数型不等式、对数型不等式的求解及指数函数的值域问题,集合的基本运算.

练习册系列答案
相关题目
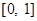 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数 称为
称为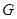 函数。
函数。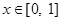 ,总有
,总有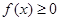 ;
; 时,总有
时,总有 成立。
成立。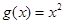 与
与 是定义在
是定义在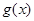 是否为
是否为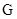 函数?并说明理由;
函数?并说明理由; 是
是 的值;
的值;
 解的个数情况。
解的个数情况。 千件,需另投入成本为
千件,需另投入成本为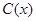 ,当年产量不足80千件时,
,当年产量不足80千件时, (万元).当年产量不小于80千件时,
(万元).当年产量不小于80千件时,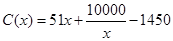 (万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完. (万元)关于年产量
(万元)关于年产量 ,
, ,且
,且 的解集为
的解集为 .
. 的值;
的值; ,且
,且 ,求证:
,求证:
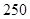 万元,每生产
万元,每生产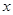 千件,需另投入成本为
千件,需另投入成本为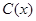 .当年产量不足
.当年产量不足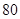 千件时,
千件时,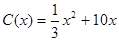 (万元).当年产量不小于
(万元).当年产量不小于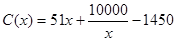 (万元).每件商品售价为
(万元).每件商品售价为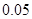 万元.通过市场分析,该厂生产的商品能全部售完.
万元.通过市场分析,该厂生产的商品能全部售完.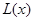 (万元)关于年产量
(万元)关于年产量 上的单调函数
上的单调函数 满足
满足 ,且对任意
,且对任意 都有
都有
 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
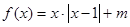
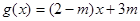 ,若方程
,若方程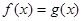 在
在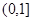 上有且仅一个实根,求实数
上有且仅一个实根,求实数 的取值范围;
的取值范围;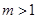 时,求函数
时,求函数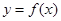 在
在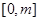 上的最大值.
上的最大值. .
. 时,求
时,求 的值域;
的值域; ,当
,当 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.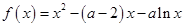 .
. 的单调区间
的单调区间 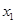 、
、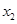 ,且
,且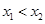 ,求证:
,求证: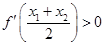 .
.