题目内容
已知函数 .
.
(Ⅰ)若 时,求
时,求 的值域;
的值域;
(Ⅱ)若存在实数 ,当
,当 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(I) 的值域为:
的值域为: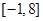 .(II)
.(II)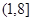 .
.
解析试题分析:(I)将二次函数 配方,结合抛物线的图象便可得
配方,结合抛物线的图象便可得 的值域.
的值域.
(II)由 恒成立得:
恒成立得: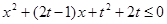 恒成立,
恒成立,
令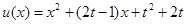 ,
,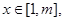 则只需
则只需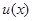 的最大值小于等于0.
的最大值小于等于0.
由此得: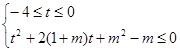 ,令
,令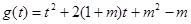
则原题可转化为:存在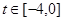 ,使得
,使得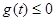 .这又需要
.这又需要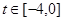 时
时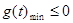 .接下来又对二次函数
.接下来又对二次函数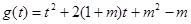 分情况讨论,从而求出实数
分情况讨论,从而求出实数 的取值范围.
的取值范围.
试题解析:(I)将二次函数 配方得:
配方得: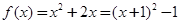 2分
2分
该函数的图象是一条开口向上的抛物线,顶点为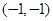 ,
,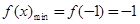 .
.
因为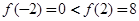 ,所以
,所以 最大值为
最大值为 ,
,
∴ 的值域为:
的值域为: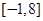 6分
6分
(II)由 恒成立得:
恒成立得: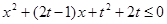 恒成立,
恒成立,
令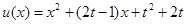 ,
,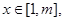 因为抛物线的开口向上,所以
因为抛物线的开口向上,所以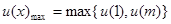 ,由
,由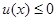 恒成立知:
恒成立知: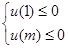 8分
8分
化简得: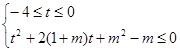 令
令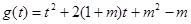
则原题可转化为:存在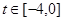 ,使得
,使得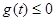 即:当
即:当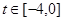 ,
,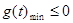 10分
10分
∵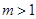 ,
,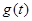 的对称轴:
的对称轴: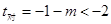
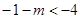 即:
即: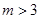 时,
时,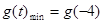
∴
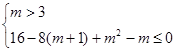 解得:
解得: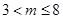
②当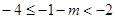 即:
即: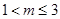 时,
时,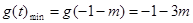
∴
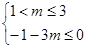 解得:
解得: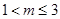
综上: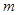 的取值范围为:
的取值范围为: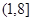 13分
13分
法二:也可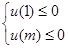 ,
,
化简得: 有解.
有解.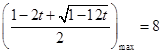 ,则
,则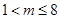 .
.
考点:1、二次函数;2、函数的最值;3、解不等式.

练习册系列答案
 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
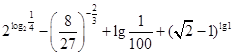
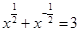 ,求
,求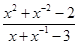 的值.
的值.
 .
. ,集合
,集合 ,求
,求 ,
,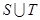 .
. =
= ,
, =
= ,若曲线
,若曲线 和曲线
和曲线 都过点P(0,2),且在点P处有相同的切线
都过点P(0,2),且在点P处有相同的切线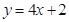 .
. ,
, ,
, ,
, 的值;
的值; 时,
时, ≤
≤ ,求
,求 的取值范围.
的取值范围. 的定义域为
的定义域为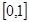 ,且同时满足以下三个条件:①
,且同时满足以下三个条件:①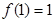 ;②对任意的
;②对任意的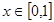 ,都有
,都有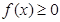 ;③当
;③当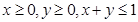 时总有
时总有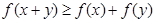 .
.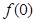 的值;
的值;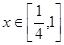 时,恒有
时,恒有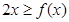 .
. ;
; .
.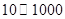 万元的投资收益.现公司准备制定一个对科研课题组的奖励方案:奖金
万元的投资收益.现公司准备制定一个对科研课题组的奖励方案:奖金 (单位:万元)随投资收益
(单位:万元)随投资收益 (单位:万元)的增加而增加,且奖金不低于
(单位:万元)的增加而增加,且奖金不低于 万元,同时不超过投资收益的
万元,同时不超过投资收益的 .
. ,试用数学语言表述公司对奖励方案的函数模型
,试用数学语言表述公司对奖励方案的函数模型 ; ②
; ②
 ,
, 时,解不等式
时,解不等式
 有最大值
有最大值 ,求实数
,求实数 的值.
的值. .若
.若 的定义域为
的定义域为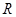 ,求实数
,求实数 的取值范围.
的取值范围.