题目内容
定义在 上的单调函数
上的单调函数 满足
满足 ,且对任意
,且对任意 都有
都有
(1)求证: 为奇函数;
为奇函数;
(2)若 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(1)证明见试题解析;(2)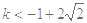 .
.
解析试题分析:(1)这是抽象函数问题,要证明它是奇函数,当然要根据奇函数的定义,证明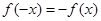 或
或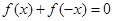 ,由此在已知式
,由此在已知式 里设
里设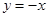 ,从而有
,从而有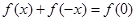 ,因此我们还要先求出
,因此我们还要先求出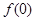 ,这个只要设
,这个只要设 或者有一个为0即可得
或者有一个为0即可得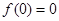 ,故可证得
,故可证得 为奇函数;(2)不等式
为奇函数;(2)不等式 可以利用
可以利用 为奇函数的结论,变形为
为奇函数的结论,变形为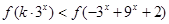 ,再利用函数的单调性去掉符号“
,再利用函数的单调性去掉符号“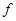 ”,转化为关于
”,转化为关于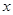 的不等式恒成立问题,即
的不等式恒成立问题,即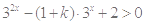 对任意
对任意 成立,这时还需要用换元法(设
成立,这时还需要用换元法(设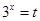 )变化二次不等式怛成立,当然不要忘记
)变化二次不等式怛成立,当然不要忘记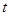 的取值范围.
的取值范围.
试题解析:(Ⅰ)证明:∵ 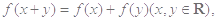 ①
①
令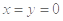 ,代入①式,得
,代入①式,得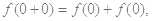 即
即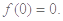
令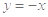 ,代入①式,得
,代入①式,得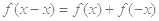 ,又
,又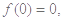
则有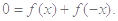 即
即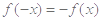 对任意
对任意 成立,
成立,
所以 是奇函数. 4分
是奇函数. 4分
(Ⅱ)解: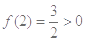 ,即
,即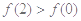 ,又
,又 在
在 上是单调函数,
上是单调函数,
所以 在
在 上是增函数.
上是增函数.
又由(1) 是奇函数.
是奇函数.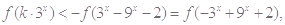
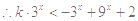 ,即
,即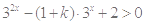 对任意
对任意 成立.
成立.
令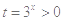 ,问题等价于
,问题等价于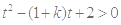 对任意
对任意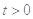 恒成立. 8分
恒成立. 8分
令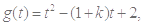 其对称轴
其对称轴 .
.
当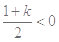 时,即
时,即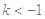 时,
时,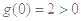 ,符合题意; 10分
,符合题意; 10分
当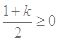 时,对任意
时,对任意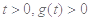 恒成立
恒成立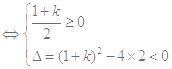
解得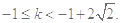 12分
12分
综上所述,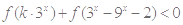 对任意
对任意 恒成立时,
恒成立时,
实数 的取值范围是:
的取值范围是: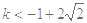 . 13分
. 13分
考点:(1)奇函数的定义;;(2)不等式恒成立问题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
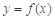 满足:当
满足:当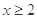 时,
时,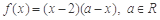 ,当
,当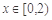 时,
时,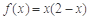 .
.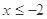 时,
时,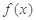 的表达式;
的表达式;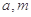 满足什么条件时,函数
满足什么条件时,函数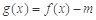 有4个零点,且这4个零点从小到大依次构成等差数列.
有4个零点,且这4个零点从小到大依次构成等差数列.
 ,求
,求 的值.
的值.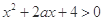 ,对一切
,对一切 恒成立;命题q:函
恒成立;命题q:函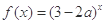 是增函数.若p或q为真,p且q为假,求实数a的取值范围.
是增函数.若p或q为真,p且q为假,求实数a的取值范围.
 .
. ,集合
,集合 ,求
,求 ,
,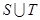 .
. 的解集为M,求当x∈M时函数
的解集为M,求当x∈M时函数 的最大、最小值.
的最大、最小值. =
= ,
, =
= ,若曲线
,若曲线 和曲线
和曲线 都过点P(0,2),且在点P处有相同的切线
都过点P(0,2),且在点P处有相同的切线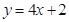 .
. ,
, ,
, ,
, 的值;
的值; 时,
时, ≤
≤ ,求
,求 的取值范围.
的取值范围. ;
; .
. 辟为水果园,其中
辟为水果园,其中 ,
, 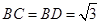 ,
, .若经过
.若经过 上一点
上一点 和
和 上一点
上一点 铺设一条道路
铺设一条道路 ,且
,且 .
.
 的关系式;
的关系式; 的位置在哪里?
的位置在哪里?