题目内容
某厂生产某种产品的年固定成本为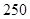 万元,每生产
万元,每生产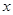 千件,需另投入成本为
千件,需另投入成本为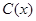 .当年产量不足
.当年产量不足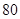 千件时,
千件时,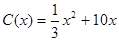 (万元).当年产量不小于
(万元).当年产量不小于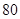 千件时,
千件时,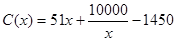 (万元).每件商品售价为
(万元).每件商品售价为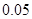 万元.通过市场分析,该厂生产的商品能全部售完.
万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润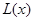 (万元)关于年产量
(万元)关于年产量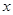 (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
(1) ;
;
(2)当产量为100 千件时,该厂在这一商品中所获利润最大,最大利润为1000 万元.
解析试题分析:(1)根据题意分 时,
时, 时,分别确定函数的解析式,得到分段函数以
时,分别确定函数的解析式,得到分段函数以 ;
;
(2)分别确定 时,,
时,, 时,函数的最大值,并加以比较.确定函数的最大值时,应用了二次函数的性质及基本不等式.
时,函数的最大值,并加以比较.确定函数的最大值时,应用了二次函数的性质及基本不等式.
试题解析:
(1) 因为每件商品售价为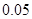 万元,则
万元,则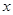 千件商品销售额为0.05×1000x万元,依题意得:
千件商品销售额为0.05×1000x万元,依题意得:
当 时,
时,
= 2分
2分
当 时,
时,
=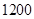 -
- . 4分
. 4分
以 6分
6分
(2)当 时,
时, .
.
此时,当 时,
时, 取得最大值
取得最大值 万元. 9分
万元. 9分
当 时,
时,
此时,当 时,即
时,即 时,
时, 取得最大值1000万元. 12分
取得最大值1000万元. 12分
∵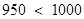
所以,当产量为100 千件时,该厂在这一商品中所获利润最大,最大利润为1000万元. 13分
考点:函数应用问题,分段函数,二次函数的性质,基本不等式.

练习册系列答案
相关题目
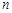 个工作台,将工艺流水线用如图
个工作台,将工艺流水线用如图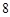 所示的数轴表示,各工作台的坐标分别为
所示的数轴表示,各工作台的坐标分别为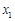 ,
,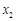 ,
,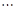 ,
,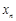 ,每个工作台上有若干名工人.现要在流水线上建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.
,每个工作台上有若干名工人.现要在流水线上建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.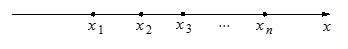
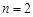 ,每个工作台上只有一名工人,试确定供应站的位置;
,每个工作台上只有一名工人,试确定供应站的位置;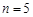 ,工作台从左到右的人数依次为
,工作台从左到右的人数依次为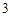 ,
,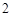 ,
,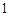 ,
,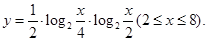
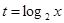 ,求
,求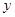 关于
关于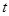 的函数关系式及
的函数关系式及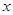 的值.
的值.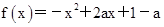 在
在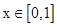 时有最大值2,求a的值.
时有最大值2,求a的值.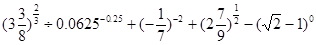
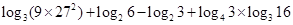

 .
. ,集合
,集合 ,求
,求 ,
,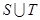 .
.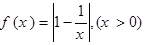
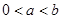 ,且
,且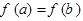 时,求证:
时,求证: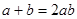
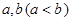 ,使得函数
,使得函数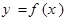 的定义域、值域都是
的定义域、值域都是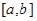 ?若存在,则求出
?若存在,则求出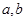 的值,若不存在,请说明理由.
的值,若不存在,请说明理由. 的定义域为
的定义域为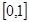 ,且同时满足以下三个条件:①
,且同时满足以下三个条件:①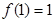 ;②对任意的
;②对任意的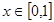 ,都有
,都有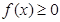 ;③当
;③当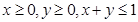 时总有
时总有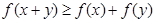 .
.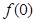 的值;
的值;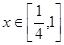 时,恒有
时,恒有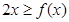 .
.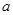 为实数,函数
为实数,函数 。
。 ,求
,求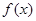 的最小值;
的最小值;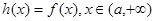 ,直接写出(不需给出演算步骤)不等式
,直接写出(不需给出演算步骤)不等式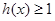 的解集.
的解集.