题目内容
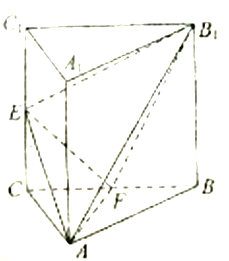
【题目】在如图所示的多面体中, ![]() 平面
平面![]()
![]() .
.

(Ⅰ)在![]() 上求作
上求作![]() ,使
,使![]() 平面
平面![]() ,请写出作法并说明理由;
,请写出作法并说明理由;
(Ⅱ)若![]() 在平面
在平面![]() 的正投影为
的正投影为![]() ,求四面体
,求四面体![]() 的体积.
的体积.
【答案】(1)见解析(2)![]()
【解析】试题分析:(Ⅰ)本问为探索性问题,考查直线与平面平行,可以通过线面平行判定定理证明,也可以通过面面平行来证明线面平行,根据本题实际条件,可以选择先证明面面平行,根据底面为等腰梯形且![]() ,取
,取![]() 中点
中点![]() ,易证四边形
,易证四边形![]() 为平行四边形,所以可以证明出平面
为平行四边形,所以可以证明出平面![]() 平面
平面![]() ,则
,则![]() 与
与![]() 交点即为所求点
交点即为所求点![]() ,易证
,易证![]() 平面
平面![]() ;(Ⅱ)本问主要是找到
;(Ⅱ)本问主要是找到![]() 点在平面
点在平面![]() 内的正投影
内的正投影![]() ,即过
,即过![]() 点的平面
点的平面![]() 的垂线,根据已知条件,
的垂线,根据已知条件, ![]() 平面
平面![]() ,易证明平面
,易证明平面![]() 平面
平面![]() ,因此根据面面垂直性质定理,过
,因此根据面面垂直性质定理,过![]() 点向
点向![]() 作垂线,垂足即为点
作垂线,垂足即为点![]() ,然后在底面
,然后在底面![]() 内可以求出
内可以求出![]() 的长度,再求出
的长度,再求出![]() 的面积,然后以
的面积,然后以![]() 为顶点,
为顶点, ![]() 为底面,可以求出四面体
为底面,可以求出四面体![]() 的体积.
的体积.
试题解析:(Ⅰ)取![]() 的中心
的中心![]() ,连结
,连结![]() ,交
,交![]() 于
于![]() ,
,
连结![]() ,此时
,此时![]() 为所求作的点
为所求作的点
下面给出证明:
![]() ,
, ![]() ,又
,又![]() ,
,![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
故![]() 即
即![]() .
.
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() ,
, ![]() 平面
平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
(Ⅱ) ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 平面
平面![]() .
.
过![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,则
,则![]() 平面
平面![]() 为
为![]() 在平面
在平面![]() 上的正投
上的正投
影.
在直角三角形![]() 中,得
中,得![]() ,
, ![]() ,
,
![]() ,
,
![]() .
.
所以四面体![]() 的体积为
的体积为![]() .
.

练习册系列答案
相关题目