题目内容
3.已知函数f(x)=ex(asinx+bcosx)在(0,1)处的切线与直线y=2x+e平行.(1)求a,b的值及函数f(x)的单调区间;
(2)当0<x<1时,求证:f(x)>(1+x-x2)ln(x+2)
分析 (1)求出函数的导数,求得切线的斜率,由两直线平行的条件可得a,b的方程,解得a=b=1,再由f(x)的导数,解不等式可得单调区间;
(2)先证sinx+cosx>1+x-x2,设g(x)=sinx+cosx-(1+x-x2),可通过二次求得导数,运用单调性证明;再证ex>ln(x+2),设m(x)=ex-ln(x+2)(0<x<1),求出导数判断单调性,即可得证.最后运用不等式的可乘性即可得到原不等式成立.
解答 (1)解:函数f(x)=ex(asinx+bcosx)的导数为
f′(x)=ex[(a-b)sinx+(a+b)cosx],
在(0,1)处的切线与直线y=2x+e平行,
则有f(0)=1,f′(0)=2,
即为b=1,a+b=2,
解得a=b=1;
f(x)=ex(sinx+cosx)的导数为f′(x)=2ex•cosx,
由f′(x)>0可得cosx>0,即为2kπ-$\frac{π}{2}$<x<2kπ+$\frac{π}{2}$,k∈Z,
由f′(x)<0可得cosx<0,即为2kπ+$\frac{π}{2}$<x<2kπ+$\frac{3π}{2}$,k∈Z,
则f(x)的增区间为(2kπ-$\frac{π}{2}$,2kπ+$\frac{π}{2}$)k∈Z,
减区间为(2kπ+$\frac{π}{2}$,2kπ+$\frac{3π}{2}$),k∈Z;
(2)证明:由0<x<1可设g(x)=sinx+cosx-(1+x-x2),
g′(x)=cosx-sinx-1+2x,
令h(x)=cosx-sinx-1+2x,
h′(x)=-sinx-cosx+2=2-$\sqrt{2}sin(x+\frac{π}{4})$>0恒成立.
h(x)在(0,1)递增.即有h(0)<h(x),
即为h(x)>0,即为g′(x)=cosx-sinx-1+2x>0,
g(x)在(0,1)递增,即有g(x)>g(0)=0,
则当0<x<1时,sinx+cosx>1+x-x2①
又设m(x)=ex-ln(x+2)(0<x<1),
m′(x)=ex-$\frac{1}{x+2}$,当0<x<1时,m′(x)>0恒成立,
即有m(x)在(0,1)递增,
即m(x)>m(0)>0,
即有ex>ln(x+2)②
由①②可得ex(sinx+cosx)>(1+x-x2)ln(x+2),
故当0<x<1时,f(x)>(1+x-x2)ln(x+2).
点评 本题考查导数的运用:求切线的斜率和单调区间,主要考查函数的单调性的运用,同时考查不等式的证明,注意运用构造函数通过导数判断单调性,以及不等式的性质是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 相交 | B. | 外切 | C. | 内切 | D. | 相交或内切 |
| A. | {x|x<1} | B. | {x|x>1} | C. | {x|0<x<1} | D. | ∅ |
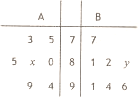 某学校从A、B两个班级中各选出7名学生参加市级比赛,他们去得的成绩(满分100分)的茎叶如图所示,其中A班学生成绩的众数是85,B班学生成绩的中位数是83.则x+y的值为8.
某学校从A、B两个班级中各选出7名学生参加市级比赛,他们去得的成绩(满分100分)的茎叶如图所示,其中A班学生成绩的众数是85,B班学生成绩的中位数是83.则x+y的值为8.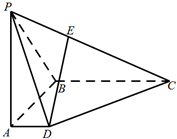 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,∠DAB=90°,PA=AB=BC=3,AD=1.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,∠DAB=90°,PA=AB=BC=3,AD=1. 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为6.
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为6.