题目内容
2.设等差数列{an}和等比数列{bn}首项都是1,公差和公比都是2,则a${\;}_{{b}_{2}}$+a${\;}_{{b}_{3}}$+a${\;}_{{b}_{4}}$=( )| A. | 24 | B. | 25 | C. | 26 | D. | 27 |
分析 利用等比数列求出b2,b3,b4,然后利用等差数列求解即可.
解答 解:等比数列{bn}首项是1,公比是2,
∴b2=2,b3=4,
b4=8,
等差数列{an}首项是1,公差是2,
∴a${\;}_{{b}_{2}}$+a${\;}_{{b}_{3}}$+a${\;}_{{b}_{4}}$=a2+a4+a8=3a1+11d=3+11×2=25.
故选:B.
点评 本题考查等差数列以及等比数列的通项公式的应用,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.实数x,y满足$\left\{\begin{array}{l}{2x-y≥0}\\{y≥x}\\{y≥-x+b}\end{array}\right.$,则z=2x+y的最小值为3,则实数b的值为( )
| A. | $\frac{4}{9}$ | B. | -$\frac{4}{9}$ | C. | $\frac{9}{4}$ | D. | -$\frac{9}{4}$ |
10.命题p:关于x的方程x|x|-2x+m=0(m∈R)有三个实数根;命题q:0≤m<1;则命题p成立是命题q成立的( )
| A. | 充分而不必要的条件 | B. | 必要而不充分的条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要的条件 |
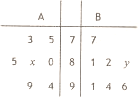 某学校从A、B两个班级中各选出7名学生参加市级比赛,他们去得的成绩(满分100分)的茎叶如图所示,其中A班学生成绩的众数是85,B班学生成绩的中位数是83.则x+y的值为8.
某学校从A、B两个班级中各选出7名学生参加市级比赛,他们去得的成绩(满分100分)的茎叶如图所示,其中A班学生成绩的众数是85,B班学生成绩的中位数是83.则x+y的值为8.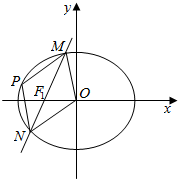 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右顶点、上顶点分别为A、B,坐标原点到直线AB的距离为$\frac{{4\sqrt{3}}}{3}$,且$a=\sqrt{2}b$.
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右顶点、上顶点分别为A、B,坐标原点到直线AB的距离为$\frac{{4\sqrt{3}}}{3}$,且$a=\sqrt{2}b$.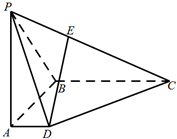 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,∠DAB=90°,PA=AB=BC=3,AD=1.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,∠DAB=90°,PA=AB=BC=3,AD=1.