题目内容

19．（x-1）（$\frac{1}{x}$-1）5的展开式中的常数项是6．

分析 把（$\frac{1}{x}$-1）5的按照二项式定理展开，可得（x-1）（$\frac{1}{x}$-1）5的展开式中的常数项．

解答 解：由于（x-1）（$\frac{1}{x}$-1）5=（x-1）（${C}_{5}^{0}$•${（\frac{1}{x}）}^{5}$-${C}_{5}^{1}$•${（\frac{1}{x}）}^{4}$+${C}_{5}^{2}$•${（\frac{1}{x}）}^{3}$-${C}_{5}^{3}$•${（\frac{1}{x}）}^{2}$+${C}_{5}^{4}$•$\frac{1}{x}$-${C}_{5}^{5}$ ），
∴（x-1）（$\frac{1}{x}$-1）5的展开式中的常数项是${C}_{5}^{4}$+1=6，
故答案为：6．

点评 本题主要考查二项式定理的应用，二项展开式的通项公式，求展开式中某项的系数，属于基础题．

练习册系列答案
相关题目
9．设点P为圆O：x2+y2=4上的一动点，点Q为点P在x轴上的射影，动点M满足：$\overrightarrow{MQ}$=$\frac{1}{2}$$\overrightarrow{PQ}$．
（1）求动点M的轨迹E的方程；
（2）过点F（-$\sqrt{3}$，0）作直线l交圆O于A、B两点，交（1）中的轨迹E于点C、D两点，问：是否存在这样的直线l，使得$\sqrt{|AF|•|BF|}$=$\frac{|CF|+|DF|}{2}$成立？若存在，求出所有的直线l的方程；若不存在，请说明理由．
10．（1）求$\frac{1}{{C}_{n}^{3}}$-$\frac{1}{{C}_{n}^{4}}$＜$\frac{1}{{C}_{n}^{12}}$的解集．
（2）设[x]表示不超过x的最大整数.${C}_{n}^{x}$=$\frac{n（n-1）…（n-[x]+1）}{x（x-1）…（x-[x]+1）}$，x∈[1，+∞）．若x∈[$\frac{3}{2}$，3]，求C${\;}_{8}^{x}$值域．
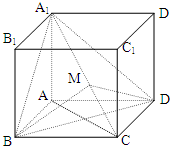7．如图，长方体ABCD-A1B1C1D1的AA1=1，底面ABCD的周长为4．
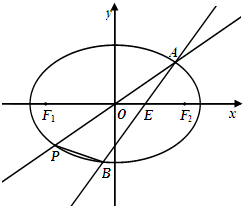（1）当长方体ABCD-A1B1C1D1的体积最大时，求直线BA1与平面A1CD所成角；
（2）线段A1C上是否存在一点P，使得A1C⊥平面BPD，若有，求出P点的位置，没有请说明理由．
14．如图，在平面直角坐标系xoy中，椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的离心率为$\frac{{\sqrt{6}}}{3}$，直线l与x轴交于点E，与椭圆C交于A、B两点．当直线l垂直于x轴且点E为椭圆C的右焦点时，弦AB的长为$\frac{{2\sqrt{6}}}{3}$．
（1）求椭圆C的方程；
（2）是否存在点E，使得$\frac{1}{{E{A^2}}}+\frac{1}{{E{B^2}}}$为定值？若存在，请指出点E的坐标，并求出该定值；若不存在，请说明理由．
4．某次足球赛共12支球队参加，分三个阶段进行．
（1）小组赛：经抽签分成甲、乙两组，每组6队进行单循环比赛，以几分及净胜球数取前两名；
（2）半决赛：甲组第一名与乙组第二名，乙组第一名与甲组第二名作主、客场交叉淘汰赛（每两队主、客场各赛一场）决出胜者；
（3）决赛：两个胜队参加决赛一场，决出胜负．
问：全部赛程共需比赛多少场？
11．计算：log2$\sqrt{\frac{7}{72}}$+log26-$\frac{1}{2}$log228．
8．已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1（a＞b＞0$）的离心率是$\frac{\sqrt{2}}{2}$，A1，A2是椭圆E的长轴的两个端点（A2位于A1右侧），B是椭圆在y轴正半轴上的顶点，点F是椭圆E的右焦点，点M是x轴上位于A2右侧的一点，且$\frac{1}{|FM|}$是$\frac{1}{|{A}_{1}M|}$与$\frac{1}{|{A}_{2}M|}$的等差中项，|FM|=1．
（1）求椭圆E的方程以及点M的坐标；
（2）是否存在经过点（0，$\sqrt{2}$）且斜率为k的直线l与椭圆E交于不同的两点P和Q，使得向量$\overrightarrow{OP}$+$\overrightarrow{OQ}$与$\overrightarrow{{A}_{2}B}$共线？若存在，求出直线l的方程；如果不存在，请说明理由．
16．已知函数f（x）=lg$\frac{1+x}{1-x}$，则“x＜$\frac{9}{11}$”是“f（x）＜1成立的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网