题目内容
4．某次足球赛共12支球队参加，分三个阶段进行．（1）小组赛：经抽签分成甲、乙两组，每组6队进行单循环比赛，以几分及净胜球数取前两名；
（2）半决赛：甲组第一名与乙组第二名，乙组第一名与甲组第二名作主、客场交叉淘汰赛（每两队主、客场各赛一场）决出胜者；
（3）决赛：两个胜队参加决赛一场，决出胜负．
问：全部赛程共需比赛多少场？
分析 先计算出（1）小组赛，（2）半决赛，（3）决赛的场数，根根据分类计数原理即可得到总场数．
解答 解：（1）小组赛中每组6队进行单循环比赛，就是6支球队的任两支球队都要比赛一次，所需比赛的场次即为从6个元素中任取2个元素的组合数，所以小组赛共要比赛2C62=30场．（2）半决赛中甲组第一名与乙组第二名（或乙组第一名与甲组第二名）主客场各赛一场，所需比赛的场次即为从2个元素中任取2个元素的排列数，所以半决赛共要比赛2A22=4场．
（3）决赛只需比赛1场，即可决出胜负．
所以全部赛程共需比赛30+4+1=35场．
点评 本题考查了分类计数原理，关键是求出每种比赛需要的场次，属于中档题．
练习册系列答案
赢在课堂名师课时计划系列答案
相关题目
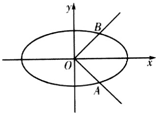已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的离心率为$\frac{{\sqrt{6}}}{3}$，点O为坐标原点，椭圆C与曲线|y|=x的交点分别为A，B（A在第四象限），且$\overrightarrow{OB}•\overrightarrow{AB}=\frac{3}{2}$．