题目内容
7. 如图,长方体ABCD-A1B1C1D1的AA1=1,底面ABCD的周长为4.
如图,长方体ABCD-A1B1C1D1的AA1=1,底面ABCD的周长为4.(1)当长方体ABCD-A1B1C1D1的体积最大时,求直线BA1与平面A1CD所成角;
(2)线段A1C上是否存在一点P,使得A1C⊥平面BPD,若有,求出P点的位置,没有请说明理由.
分析 (1)先设AB=b,AD=2-b,分别以AB,AD,AA1三直线为x,y,z轴,建立空间直角坐标系,从而可写出空间一些点的坐标,根据条件即可求出b=1.设平面A1CD的法向量为$\overrightarrow{{n}_{1}}=({x}_{1},{y}_{1},{z}_{1})$,根据$\left\{\begin{array}{l}{\overrightarrow{{n}_{1}}•\overrightarrow{CD}=0}\\{\overrightarrow{{n}_{1}}•\overrightarrow{C{A}_{1}}=0}\end{array}\right.$即可求出法向量$\overrightarrow{{n}_{1}}$,设直线BA1和平面A1CD所成角为θ,由sin$θ=|cos<\overrightarrow{B{A}_{1}},\overrightarrow{{n}_{1}}>|$即可求出θ;
(2)设存在P点满足条件,设P(x,y,z),从而有$\overrightarrow{{A}_{1}P}=t\overrightarrow{{A}_{1}C}$,这样即可用t,b表示出P点坐标,而根据$\left\{\begin{array}{l}{\overrightarrow{{A}_{1}C}•\overrightarrow{BP}=0}\\{\overrightarrow{{A}_{1}C}•\overrightarrow{BD}=0}\end{array}\right.$即可求出b,t,从而能够确定出P点的位置.
解答 解:设AB=b,则AD=2-b,分别以边AB,AD,AA1所在直线为x,y,z轴,建立如图所示空间直角坐标系,则: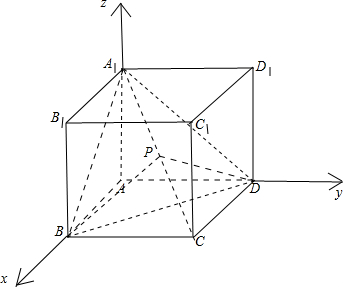 A(0,0,0),B(b,0,0),C(b,2-b,0),D(0,2-b,0),A1(0,0,1);
A(0,0,0),B(b,0,0),C(b,2-b,0),D(0,2-b,0),A1(0,0,1);
(1)根据条件,2(AB+AD)=4;
∴2=AB+AD≥2$\sqrt{AB•AD}$;
∴AB•AD≤1,当AB=AD=1时取“=”,∴此时b=1,B(1,0,0),C(1,1,0),D(0,1,0);
∴$\overrightarrow{B{A}_{1}}=(-1,0,1)$,$\overrightarrow{CD}=(-1,0,0)$,$\overrightarrow{C{A}_{1}}=(-1,-1,1)$,设平面A1CD的法向量为$\overrightarrow{{n}_{1}}=({x}_{1},{y}_{1},{z}_{1})$,则:
$\left\{\begin{array}{l}{\overrightarrow{{n}_{1}}•\overrightarrow{CD}=-{x}_{1}=0}\\{\overrightarrow{{n}_{2}}•\overrightarrow{C{A}_{1}}=-{x}_{1}-{y}_{1}+{z}_{1}=0}\end{array}\right.$;
取z1=1,则$\overrightarrow{{n}_{1}}=(0,1,1)$;
设直线BA1与平面A1CD所成角为θ,则:
sinθ=$|cos<\overrightarrow{B{A}_{1}},\overrightarrow{{n}_{1}}>|$=$\frac{1}{\sqrt{2}•\sqrt{2}}=\frac{1}{2}$;
∴θ=30°;
即直线BA1和平面A1CD所成角为30°;
(2)假设在线段A1C上存在点P满足条件,设P(x,y,z),∴存在t,使$\overrightarrow{{A}_{1}P}=t\overrightarrow{{A}_{1}C}$;
∴(x,y,z-1)=t(b,2-b,-1);
∴P(bt,(2-b)t,1-t),$\overrightarrow{BP}=(b(t-1),(2-b)t,1-t)$,$\overrightarrow{BD}=(-b,2-b,0)$;
∴$\left\{\begin{array}{l}{\overrightarrow{{A}_{1}C}•\overrightarrow{BP}=0}\\{\overrightarrow{{A}_{1}C}•\overrightarrow{BD}=0}\end{array}\right.$;
∴$\left\{\begin{array}{l}{3t-b-1=0}\\{2-2b=0}\end{array}\right.$;
∴$b=1,t=\frac{2}{3}$;
即只有当底面四边形是正方形时才有符合要求的点P,位置是线段A1C上A1P:PC=2:1处.
点评 考查通过建立空间直角坐标系,利用空间向量求线面角,解决线面垂直问题的方法,基本不等式的运用,长方体的体积公式,以及平面法向量的概念及求法,直线和平面所成角与直线方向向量和平面法向量夹角的关系,向量夹角余弦的坐标公式,线面垂直的性质,两向量垂直的充要条件.

| A. | $\frac{5\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{5}{2}$ | D. | 5 |
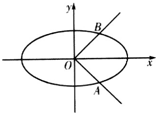 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{6}}}{3}$,点O为坐标原点,椭圆C与曲线|y|=x的交点分别为A,B(A在第四象限),且$\overrightarrow{OB}•\overrightarrow{AB}=\frac{3}{2}$.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{6}}}{3}$,点O为坐标原点,椭圆C与曲线|y|=x的交点分别为A,B(A在第四象限),且$\overrightarrow{OB}•\overrightarrow{AB}=\frac{3}{2}$. 设椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1、F2,短轴长为2,离心率为$\frac{\sqrt{3}}{2}$.
设椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1、F2,短轴长为2,离心率为$\frac{\sqrt{3}}{2}$.