题目内容
【题目】已知抛物线![]() 过点
过点![]() ,直线
,直线![]() 过点
过点![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
, ![]() 两点.点
两点.点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,连接
,连接![]() .
.

(1)求抛物线线![]() 的标准方程;
的标准方程;
(2)问直线![]() 是否过定点?若是,求出定点坐标;若不是,请说明理由.
是否过定点?若是,求出定点坐标;若不是,请说明理由.
【答案】(1) ![]() ;(2)答案见解析.
;(2)答案见解析.
【解析】试题分析:(1)利用点的坐标在曲线上,代入求解即可;(2)设直线l的方程为y=kx﹣1,又设A(x1,y1),B(x2,y2),则A'(﹣x1,y1),联立直线与抛物线方程,利用韦达定理以及判别式,求出直线的斜率,推出直线方程,利用直线系求解即可.
解析:
(1)将点![]() 代入抛物线
代入抛物线![]() 的方程得,
的方程得,
![]() .
.
所以,抛物线![]() 的标准方程为
的标准方程为![]() .
.
(2)设直线![]() 的方程为
的方程为![]() ,又设
,又设![]() ,
, ![]() ,则
,则![]() .由
.由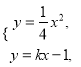 得
得![]() .
.
则![]() ,
, ![]() ,
, ![]() .
.
所以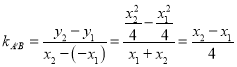 .
.
于是直线![]() 的方程为
的方程为![]() .
.
所以![]() .
.
当![]() 时,
时, ![]() ,
,
所以直线![]() 过定点
过定点![]() .
.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
【题目】某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据:
x | 6 | 8 | 10 | 12 |
y | 2 | 3 | 5 | 6 |
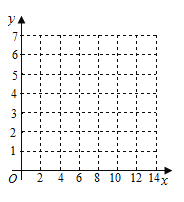
(1)请在图中画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(3)试根据(2)求出的线性回归方程,预测记忆力为9的同学的判断力.