题目内容
【题目】已知函数![]() 若函数
若函数![]() 恰有
恰有![]() 个不同的零点,则实数
个不同的零点,则实数![]() 的取值范围是__________.
的取值范围是__________.
【答案】(3/2,2)
【解析】g(x)=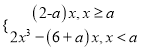 ,
,
显然,当a=2时,g(x)有无穷多个零点,不符合题意;
当x≥a时,令g(x)=0得x=0,
当x<a时,令g(x)=0得x=0或x2=![]() ,
,
(1)若a>0且a≠2,则g(x)在[a,+∞)上无零点,在(﹣∞,a)上存在零点x=0和x=-![]() ,∴
,∴![]() ≥a,解得0<a<2,
≥a,解得0<a<2,
(2)若a=0,则g(x)在[0,+∞)上存在零点x=0,在(﹣∞,0)上存在零点x=﹣![]() ,
,
符合题意;
(3)若a<0,则g(x)在[a,+∞)上存在零点x=0,
∴g(x)在(﹣∞,a)上只有1个零点,∵0(﹣∞,a),∴g(x)在(﹣∞,a)上的零点为x=﹣![]() ,
,
∴﹣![]() <a,解得﹣<a<0.
<a,解得﹣<a<0.
综上,a的取值范围是(![]() ,2).
,2).
故答案为(![]() ,2).
,2).

练习册系列答案
相关题目



