题目内容
19.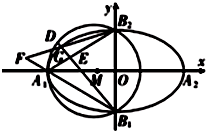 如图,已知A1,A2,B1,B2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的四个顶点,△A1B1B2的外接圆为圆M,椭圆C过点(-1,$\frac{\sqrt{6}}{3}$),($\frac{3}{2}$,$\frac{1}{2}$).
如图,已知A1,A2,B1,B2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的四个顶点,△A1B1B2的外接圆为圆M,椭圆C过点(-1,$\frac{\sqrt{6}}{3}$),($\frac{3}{2}$,$\frac{1}{2}$).(1)求椭圆C及圆M的方程;
(2)若点D是圆M劣弧$\widehat{{A}_{1}{B}_{2}}$上一动点(点D异于端点A1,B2),直线B1D分别交线段A1B2,椭圆C于点E,G,直线B2G与A1B1交于点F.
(i)求$\frac{G{B}_{1}}{E{B}_{1}}$的最大值;
(ii)E,F两点的横坐标之和是否为定值?若是,求出该定值;若不是,说明理由.
分析 (1)由已知条件椭圆C过点(-1,$\frac{\sqrt{6}}{3}$),($\frac{3}{2}$,$\frac{1}{2}$),代入,可得a,b,即可求出椭圆C的方程,由此能求出圆M的方程.
(2)(i)设直线B1D的方程为y=kx-1,与直线A1B2的方程y=$\frac{\sqrt{3}}{3}$x+1联立,解得点E,联立y=kx-1与椭圆,消去y,解得点,由此能求出$\frac{G{B}_{1}}{E{B}_{1}}$的最大值.
(ii)直线B2G的方程为y=-$\frac{1}{3k}$x+1,与直线A1B1的方程y=-$\frac{\sqrt{3}}{3}$x-1联立,解得点F,由此能求出E、F两点的横坐标之和为定值.
解答 解:(1)因为椭圆C过点(-1,$\frac{\sqrt{6}}{3}$),($\frac{3}{2}$,$\frac{1}{2}$),
∴$\left\{\begin{array}{l}{\frac{1}{{a}^{2}}+\frac{\frac{6}{9}}{{b}^{2}}=1}\\{\frac{\frac{9}{4}}{{a}^{2}}+\frac{\frac{1}{4}}{{b}^{2}}=1}\end{array}\right.$,
∴a=$\sqrt{3}$,b=1,
∴椭圆C的方程为$\frac{{x}^{2}}{3}+{y}^{2}=1$.
圆心M(-$\frac{\sqrt{3}}{3}$,0),半径A1M=$\frac{2\sqrt{3}}{3}$,
∴圆M的方程为(x+$\frac{\sqrt{3}}{3}$)2+y2=$\frac{4}{3}$.…(4分)
(2)(i)设直线B1D的方程为y=kx-1,k<-$\frac{\sqrt{3}}{3}$,
与直线A1B2的方程y=$\frac{\sqrt{3}}{3}$x+1联立,解得点E($\frac{2\sqrt{3}}{\sqrt{3}k-1}$,$\frac{\sqrt{3}k+1}{\sqrt{3}k-1}$),…(6分)
联立y=kx-1与椭圆,消去y并整理得,(1+3k2)x2-6kx=0,
解得点G($\frac{6k}{3{k}^{2}+1}$,$\frac{3{k}^{2}-1}{3{k}^{2}+1}$),…(9分)
$\frac{G{B}_{1}}{E{B}_{1}}$=$\frac{|{x}_{G}|}{|{x}_{E}|}$=1-$\frac{\sqrt{3}k+1}{3{k}^{2}+1}$
=1+$\frac{1}{-(\sqrt{3}k+1)+\frac{2}{-(\sqrt{3}k+1)}+2}$
≤1+$\frac{1}{2\sqrt{2}+2}$=$\frac{\sqrt{2}+1}{2}$,当且仅当k=-$\frac{\sqrt{6}+\sqrt{3}}{3}$时,取“=”,
∴$\frac{G{B}_{1}}{E{B}_{1}}$的最大值为$\frac{\sqrt{2}+1}{2}$.…(12分)
(ii)直线B2G的方程为y=-$\frac{1}{3k}$x+1,
与直线A1B1的方程y=-$\frac{\sqrt{3}}{3}$x-1联立,
解得点F($\frac{-6k}{\sqrt{3}k-1}$,$\frac{\sqrt{3}k+1}{\sqrt{3}k-1}$),…(14分)
∴E、F两点的横坐标之和为$\frac{2\sqrt{3}}{\sqrt{3}k-1}+\frac{-6k}{\sqrt{3}k-1}$=-2$\sqrt{3}$.
故E、F两点的横坐标之和为定值,该定值为-2$\sqrt{3}$.…(16)
点评 本题考查椭圆方程及圆的方程的求法,考查两条线段比值的最大值的求法,考查两点横坐标之各为定值的证明,解题时要认真审题,注意函数与方程思想的合理运用.

(1)m为何值时,三线共点;
(2)m=0时,三条直线能围成一个三角形吗?
(3)求当三条直线围成三角形时,m的取值范围.
| A. | 4 | B. | 3$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 8 |
 第一象限内点P在x轴、y轴上的投影分别是A和B,若矩形APBO的周长为定值2m,试证明:过P垂直于AB的直线PC恒过定点,并求出顶点坐标.
第一象限内点P在x轴、y轴上的投影分别是A和B,若矩形APBO的周长为定值2m,试证明:过P垂直于AB的直线PC恒过定点,并求出顶点坐标.