题目内容
14.已知中心在原点,焦点在坐标轴上的椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点P($\sqrt{3}$,$\frac{\sqrt{3}}{2}$),离心率为$\frac{1}{2}$,过直线l:x=4上一点M引椭圆E的两条切线,切点分别是A、B.(1)求椭圆E的方程;
(2)若在椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上的任一点N(x0,y0)处的切线方程是$\frac{{x}_{0}x}{{a}^{2}}$+$\frac{{y}_{0}y}{{b}^{2}}$=1.求证:直线AB恒过定点C,并求出定点C的坐标;
(3)是否存在实数λ,使得|AC|+|BC|=λ|AC|•|BC|恒成立?(点C为直线AB恒过的定点)若存在,求出λ的值;若不存在,请说明理由.
分析 (1)通过将点P($\sqrt{3}$,$\frac{\sqrt{3}}{2}$)代入椭圆方程,利用$\frac{c}{a}$=$\frac{1}{2}$及b2+c2=a2,计算即得结论;
(2)通过分别将点M的坐标(4,t)代入切线方程,利用两点确定唯一的一条直线,即得结论;
(3)通过将直线AB的方程代入椭圆方程,利用韦达定理计算$\frac{1}{|AC|}$+$\frac{1}{|BC|}$即可.
解答 解:(1)由椭圆E过点P($\sqrt{3}$,$\frac{\sqrt{3}}{2}$),可得$\frac{3}{{a}^{2}}$+$\frac{3}{4{b}^{2}}$=1,
又e=$\frac{c}{a}$=$\frac{1}{2}$,b2+c2=a2,
解得:a=2,b=$\sqrt{3}$.
∴椭圆E方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(2)设切点坐标为A(x1,y1),B(x2,y2),直线l上一点M的坐标(4,t),
则切线方程分别为:$\frac{{x}_{1}x}{4}+\frac{{y}_{1}y}{3}=1$、$\frac{{x}_{2}x}{4}+\frac{{y}_{2}y}{3}=1$,
又∵两切线均过点M,∴${x}_{1}+\frac{t}{3}{y}_{1}=1$、${x}_{2}+\frac{t}{3}{y}_{2}=1$,
即点A、B的坐标都适合方程$x+\frac{t}{3}y=1$,而两点确定唯一的一条直线,
故直线AB的方程是$x+\frac{t}{3}y=1$,
显然对任意实数t,点(1,0)都适合这个方程,
∴直线AB恒过定点C(1,0);
(3)结论:存在实数$λ=\frac{4}{3}$,使得|AC|+|BC|=λ|AC|•|BC|恒成立.
理由如下:
将直线AB的方程$x+\frac{t}{3}y=1$代入椭圆方程,
得:$3(-\frac{t}{3}y+1)^{2}+4{y}^{2}-12=0$,即$(\frac{{t}^{2}}{3}+4){y}^{2}-2ty-9=0$,
由韦达定理可得:y1+y2=$\frac{6t}{12+{t}^{2}}$,y1y2=-$\frac{27}{12+{t}^{2}}$,
不妨设y1>0,y2<0,
∵|AC|=$\sqrt{({x}_{1}-1)^{2}+{{y}_{1}}^{2}}$=$\sqrt{(1+\frac{{t}^{2}}{9}){{y}_{1}}^{2}}$=$\frac{\sqrt{9+{t}^{2}}}{3}$y1,同理|BC|=-$\frac{\sqrt{9+{t}^{2}}}{3}$y2,
∴$\frac{1}{|AC|}$+$\frac{1}{|BC|}$=$\frac{3}{\sqrt{9+{t}^{2}}}$($\frac{1}{{y}_{1}}$-$\frac{1}{{y}_{2}}$)=$\frac{3}{\sqrt{9+{t}^{2}}}$•$\frac{{y}_{2}-{y}_{1}}{{y}_{1}{y}_{2}}$=-$\frac{3}{\sqrt{9+{t}^{2}}}$•$\frac{\sqrt{({y}_{2}-{y}_{1})^{2}}}{{y}_{1}{y}_{2}}$
=-$\frac{3}{\sqrt{9+{t}^{2}}}$•$\frac{\sqrt{(\frac{6t}{12+{t}^{2}})^{2}+\frac{108}{12+{t}^{2}}}}{\frac{-27}{12+{t}^{2}}}$=$\frac{1}{\sqrt{9+{t}^{2}}}$•$\frac{\sqrt{144{t}^{2}+9×144}}{9}$=$\frac{4}{3}$,
即|AC|+|BC|=$\frac{4}{3}$|AC|•|BC|,
故存在实数$λ=\frac{4}{3}$,使得|AC|+|BC|=λ|AC|•|BC|恒成立.
点评 本题是一道直线与圆锥曲线的综合题,考查运算求解能力,注意解题方法的积累,属于难题.

| A. | c<b<a | B. | c<a<b | C. | a<c<b | D. | a<b<c |
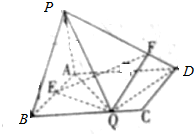 如图所示,在矩形ABCD中,AB=1,AD=a,PA⊥平面ABCD,且PA=1,E为AB中点,F、Q分别在边PD、BC上,$\overrightarrow{PF}$=λ$\overrightarrow{PD}$,λ∈(0,1),且仅存在唯一一点Q,使得PQ⊥QD.
如图所示,在矩形ABCD中,AB=1,AD=a,PA⊥平面ABCD,且PA=1,E为AB中点,F、Q分别在边PD、BC上,$\overrightarrow{PF}$=λ$\overrightarrow{PD}$,λ∈(0,1),且仅存在唯一一点Q,使得PQ⊥QD.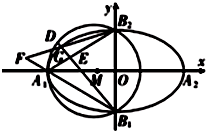 如图,已知A1,A2,B1,B2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的四个顶点,△A1B1B2的外接圆为圆M,椭圆C过点(-1,$\frac{\sqrt{6}}{3}$),($\frac{3}{2}$,$\frac{1}{2}$).
如图,已知A1,A2,B1,B2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的四个顶点,△A1B1B2的外接圆为圆M,椭圆C过点(-1,$\frac{\sqrt{6}}{3}$),($\frac{3}{2}$,$\frac{1}{2}$).