题目内容
7. 第一象限内点P在x轴、y轴上的投影分别是A和B,若矩形APBO的周长为定值2m,试证明:过P垂直于AB的直线PC恒过定点,并求出顶点坐标.
第一象限内点P在x轴、y轴上的投影分别是A和B,若矩形APBO的周长为定值2m,试证明:过P垂直于AB的直线PC恒过定点,并求出顶点坐标.
分析 设出P的坐标,求出PC的方程,判断求解即可.
解答 解:设A(a,0),则P(a,m-a),a∈(0,m),
则B(0,m-a),
PC的斜率为:$\frac{a}{m-a}$,
PC的方程为:y-(m-a)=$\frac{a}{m-a}$(x-a),
即:(m-a)y-(m-a)(m-a)-a(x-a)=0,
即:my-ay-m2+2am-ax=0,
可得my-m2-a(x+y-2m)=0,
由$\left\{\begin{array}{l}my={m}^{2}\\ x+y-2m=0\end{array}\right.$,可得$\left\{\begin{array}{l}x=m\\ y=m\end{array}\right.$,
直线PC恒过(m,m).
点评 本题考查直线系方程的应用,直线方程的求法,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.设等差数列{an}的前n项和为Sn,且满足S2014>0,S2015<0,对任意正整数n,都有|an|≥|ak|,则k的值为( )
| A. | 1006 | B. | 1007 | C. | 1008 | D. | 1009 |
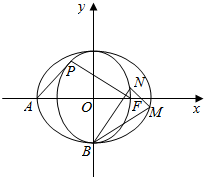 已知椭圆C1:$\frac{{x}^{2}}{2}$+y2=1和圆C2:x2+y2=1,A,B,F分别为椭圆C1左顶点、下顶点和右焦点.
已知椭圆C1:$\frac{{x}^{2}}{2}$+y2=1和圆C2:x2+y2=1,A,B,F分别为椭圆C1左顶点、下顶点和右焦点.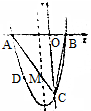
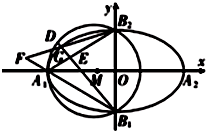 如图,已知A1,A2,B1,B2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的四个顶点,△A1B1B2的外接圆为圆M,椭圆C过点(-1,$\frac{\sqrt{6}}{3}$),($\frac{3}{2}$,$\frac{1}{2}$).
如图,已知A1,A2,B1,B2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的四个顶点,△A1B1B2的外接圆为圆M,椭圆C过点(-1,$\frac{\sqrt{6}}{3}$),($\frac{3}{2}$,$\frac{1}{2}$).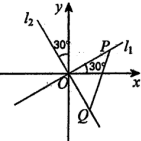 如图,两条过原点.D的直线l1,l2分别与x轴、y轴正方向成30°的角,点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动,且线段PQ的长度为2.
如图,两条过原点.D的直线l1,l2分别与x轴、y轴正方向成30°的角,点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动,且线段PQ的长度为2.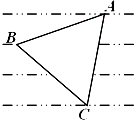 如图所示,某服装设计师要在一块条形布料上画一个等边△ABC作为点缀,使A、B、C三点分别落在条形布料的线条上,已知条形布料相邻横线间的距离为3厘米,则等边△ABC的边长应为2$\sqrt{21}$厘米.
如图所示,某服装设计师要在一块条形布料上画一个等边△ABC作为点缀,使A、B、C三点分别落在条形布料的线条上,已知条形布料相邻横线间的距离为3厘米,则等边△ABC的边长应为2$\sqrt{21}$厘米.