题目内容
11.给出三条直线l1:4x+y=4,l2:mx+y=0,l3:2x-3my=4.(1)m为何值时,三线共点;
(2)m=0时,三条直线能围成一个三角形吗?
(3)求当三条直线围成三角形时,m的取值范围.
分析 (1)求出两条直线的交点坐标代入第三条直线,求解m即可;
(2)通过m=0时,转化三条直线方程判断能围成一个三角形.
(3)由三条直线中的任意两条平行求得m的值,再由三条直线相交于一点求得m的值,则l1,l2,l3不能围成一个三角形的m的所有取值组成的集合可求.
解答 解:(1)直线l1:4x+y=4,l2:mx+y=0,的交点坐标为:(44−m44−m,-4m4−m4m4−m),
交点代入直线l3:2x-3my=4.可得:m=-1,或m=2323.此时三条直线共点.
(2)m=0时,三条直线l1:4x+y=4,l2:mx+y=0,l3:2x-3my=4.
化为三条直线l1:4x+y=4,l2:y=0,l3:x=2.
显然三条直线能够组成一个三角形.
(3)解:当直线l1:4x+y-4=0 平行于 l2:mx+y=0时,m=4.
当直线l1:4x+y-4=0 平行于 l3:2x-3my-4=0时,m=-1616,
当l2:mx+y=0 平行于 l3:2x-3my-4=0时,-m=23m23m,m无解.
当三条直线经过同一个点时,把直线l1 与l2的交点(44−m44−m,-4m4−m4m4−m)代入l3:2x-3my-4=0,解得m=-1或2323.
综上,m为4或-1616或-1或2323.三条直线不能构成三角形.
故当三条直线围成三角形时,m的取值范围(-∞,-1)∪(-1,−16−16)∪(−16−16,2323)∪(23,4)∪(4,+∞)
点评 本题考查了两直线平行的条件,考查了两直线交点坐标的求法,是中档题.

练习册系列答案
相关题目
14.某城市随机监测一年内100天的空气质量PM2.5的数据API,结果统计如下:
(1)若将API值低于150的天气视为“好天”,并将频率视为概率,根据上述表格,预测今年高考6月7日、8日两天连续出现“好天”的概率;
(2)API值对部分生产企业有着重大的影响,假设某企业的日利润f(x)与API值x的函数关系为:f(x)=\left\{\begin{array}{l}40(x≤150)\\ 15(x>150)\end{array}(单位;万元),利用分层抽样的方式从监测的100天中选出10天,再从这10天中任取3天计算企业利润之和X,求离散型随机变量X的分布列以及数学期望和方差.
| API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,+∞) |
| 天数 | 6 | 12 | 22 | 30 | 14 | 16 |
(2)API值对部分生产企业有着重大的影响,假设某企业的日利润f(x)与API值x的函数关系为:f(x)=\left\{\begin{array}{l}40(x≤150)\\ 15(x>150)\end{array}(单位;万元),利用分层抽样的方式从监测的100天中选出10天,再从这10天中任取3天计算企业利润之和X,求离散型随机变量X的分布列以及数学期望和方差.
6.已知a=log413,b=lg5,c=∫10xdx,则实数a,b,c的大小关系为( )
| A. | c<b<a | B. | c<a<b | C. | a<c<b | D. | a<b<c |

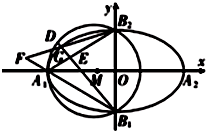 如图,已知A1,A2,B1,B2分别是椭圆C:
如图,已知A1,A2,B1,B2分别是椭圆C: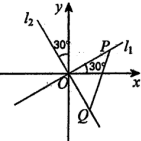 如图,两条过原点.D的直线l1,l2分别与x轴、y轴正方向成30°的角,点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动,且线段PQ的长度为2.
如图,两条过原点.D的直线l1,l2分别与x轴、y轴正方向成30°的角,点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动,且线段PQ的长度为2.