题目内容
(本小题满分14分)
已知椭圆
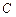 :
: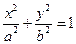
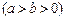 上的一动点
上的一动点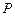 到右焦点的最短距离为
到右焦点的最短距离为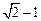 ,且右焦点到右准线的距离等于短半轴的长.
,且右焦点到右准线的距离等于短半轴的长.(Ⅰ) 求椭圆
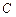 的方程;
的方程;(Ⅱ) 过点
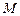 (
(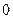 ,
,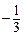 )的动直线
)的动直线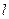 交椭圆
交椭圆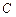 于
于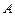 、
、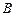 两点,试问:在坐标平面上是否存在一个定点
两点,试问:在坐标平面上是否存在一个定点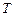 ,使得无论
,使得无论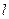 如何转动,以
如何转动,以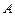
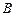 为直径的圆恒过定点
为直径的圆恒过定点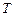 ?若存在,求出点
?若存在,求出点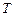 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.解: (Ⅰ)设椭圆的焦距为 ,则由题设可知
,则由题设可知 ,解此方程组得
,解此方程组得
 ,
,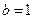 . 所以椭圆C的方程是
. 所以椭圆C的方程是 . ………5分
. ………5分
(Ⅱ)解法一:假设存在点T(u, v). 若直线l的斜率存在,设其方程为 ,
,
将它代入椭圆方程,并整理,得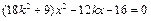
设点A、B的坐标分别为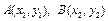 ,则
,则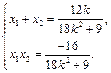 ……7分
……7分
因为 及
及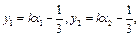
所以

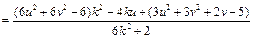 ……10分
……10分
当且仅当 恒成立时,以AB为直径的圆恒过定点T,
恒成立时,以AB为直径的圆恒过定点T,
所以 解得
解得
此时以AB为直径的圆恒过定点T(0,1). ……12分
当直线l的斜率不存在,l与y轴重合,以AB为直径的圆为 也过点T(0,1).
也过点T(0,1).
综上可知,在坐标平面上存在一个定点T(0,1),满足条件. ……14分
解法二:若直线l与y轴重合,则以AB为直径的圆是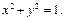
若直线l垂直于y轴,则以AB为直径的圆是
由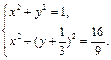 解得
解得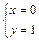 .
.
由此可知所求点T如果存在,只能是(0,1). ……8分
事实上点T(0,1)就是所求的点. 证明如下:
当直线l的斜率不存在,即直线l与y轴重合时,以AB为直径的圆为 ,
,
过点T(0,1);当直线l的斜率存在,设直线方程为 ,代入椭圆方程,并整理,得
,代入椭圆方程,并整理,得
设点A、B的坐标为 ,则
,则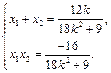 ……11分
……11分
因为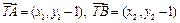 ,
,

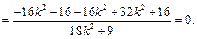
所以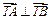 ,即以AB为直径的圆恒过定点T(0,1). ……13分
,即以AB为直径的圆恒过定点T(0,1). ……13分
综上可知,在坐标平面上存在一个定点T(0,1)满足条件. ……14分
 ,则由题设可知
,则由题设可知 ,解此方程组得
,解此方程组得 ,
,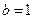 . 所以椭圆C的方程是
. 所以椭圆C的方程是 . ………5分
. ………5分(Ⅱ)解法一:假设存在点T(u, v). 若直线l的斜率存在,设其方程为
 ,
,将它代入椭圆方程,并整理,得
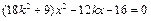
设点A、B的坐标分别为
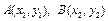 ,则
,则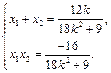 ……7分
……7分因为
 及
及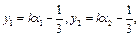
所以


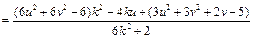 ……10分
……10分当且仅当
 恒成立时,以AB为直径的圆恒过定点T,
恒成立时,以AB为直径的圆恒过定点T,所以
 解得
解得
此时以AB为直径的圆恒过定点T(0,1). ……12分
当直线l的斜率不存在,l与y轴重合,以AB为直径的圆为
 也过点T(0,1).
也过点T(0,1).综上可知,在坐标平面上存在一个定点T(0,1),满足条件. ……14分
解法二:若直线l与y轴重合,则以AB为直径的圆是
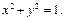
若直线l垂直于y轴,则以AB为直径的圆是

由
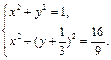 解得
解得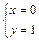 .
.由此可知所求点T如果存在,只能是(0,1). ……8分
事实上点T(0,1)就是所求的点. 证明如下:
当直线l的斜率不存在,即直线l与y轴重合时,以AB为直径的圆为
 ,
,过点T(0,1);当直线l的斜率存在,设直线方程为
 ,代入椭圆方程,并整理,得
,代入椭圆方程,并整理,得
设点A、B的坐标为
 ,则
,则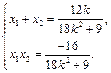 ……11分
……11分因为
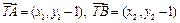 ,
,
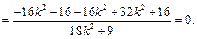
所以
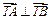 ,即以AB为直径的圆恒过定点T(0,1). ……13分
,即以AB为直径的圆恒过定点T(0,1). ……13分综上可知,在坐标平面上存在一个定点T(0,1)满足条件. ……14分

略

练习册系列答案
相关题目
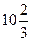 米,入水处距池边4米,同时运动员在距水面5米或5米以上时,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误。
米,入水处距池边4米,同时运动员在距水面5米或5米以上时,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误。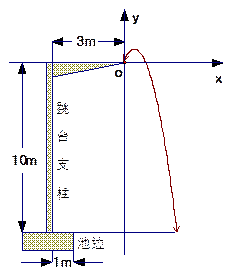
 (1)中抛物线运行,要使得此次跳水成功,他在空中调整好入水姿势时,距池边的水平距离至多应为多大?
(1)中抛物线运行,要使得此次跳水成功,他在空中调整好入水姿势时,距池边的水平距离至多应为多大?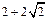 .记动点C的轨迹为曲线W.
.记动点C的轨迹为曲线W.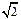 )且斜率为k的直线l与曲线W有两个不同的交点P和Q,求k的取值范围;
)且斜率为k的直线l与曲线W有两个不同的交点P和Q,求k的取值范围;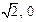 ),N(0, 1),在(Ⅱ)的条件下,是否存在常数k,使得向量
),N(0, 1),在(Ⅱ)的条件下,是否存在常数k,使得向量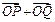 与
与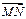 共线?如果存在,求出k的值;如果不存在,请说明理由.
共线?如果存在,求出k的值;如果不存在,请说明理由.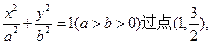
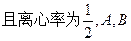 是椭圆上纵坐标不为零的两点,若
是椭圆上纵坐标不为零的两点,若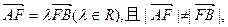 其中F为椭圆的左焦点.
其中F为椭圆的左焦点.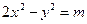 的一个焦点是
的一个焦点是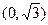 ,则
,则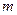 的值是__________.
的值是__________.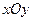 中,曲线
中,曲线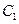 的参数方程为
的参数方程为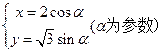 .在极坐标系(与直角坐标系
.在极坐标系(与直角坐标系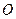 为极点,以
为极点,以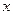 轴正半轴为极轴)中,曲线
轴正半轴为极轴)中,曲线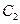 的方程为
的方程为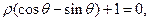 则
则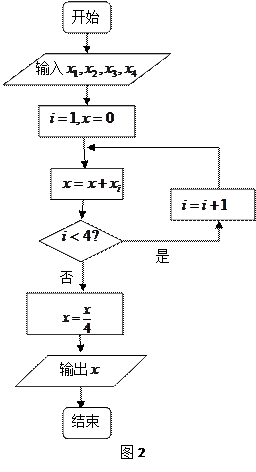
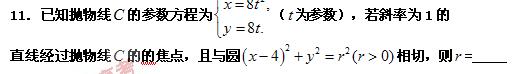
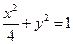 的焦点为
的焦点为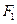 、
、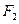 ,点
,点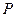 为椭圆上任意一点,过
为椭圆上任意一点,过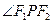 的外角平分线的垂线,垂足为点
的外角平分线的垂线,垂足为点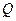 ,过点
,过点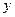 轴的垂线,垂足为
轴的垂线,垂足为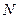 ,线段
,线段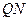 的中点为
的中点为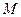 ,则点
,则点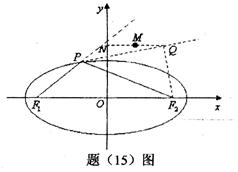
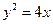 上一点
上一点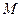 到准线的距离为3,则点
到准线的距离为3,则点 为( ▲ )
为( ▲ )