题目内容
在平面直角坐标系xOy中,已知点A(-1, 0)、B(1, 0), 动点C满足条件:△ABC的周长为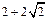 .记动点C的轨迹为曲线W.
.记动点C的轨迹为曲线W.
(Ⅰ)求W的方程;
(Ⅱ)经过点(0,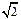 )且斜率为k的直线l与曲线W有两个不同的交点P和Q,求k的取值范围;
)且斜率为k的直线l与曲线W有两个不同的交点P和Q,求k的取值范围;
(Ⅲ)已知点M(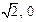 ),N(0, 1),在(Ⅱ)的条件下,是否存在常数k,使得向量
),N(0, 1),在(Ⅱ)的条件下,是否存在常数k,使得向量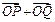 与
与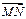 共线?如果存在,求出k的值;如果不存在,请说明理由.
共线?如果存在,求出k的值;如果不存在,请说明理由.
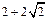 .记动点C的轨迹为曲线W.
.记动点C的轨迹为曲线W.(Ⅰ)求W的方程;
(Ⅱ)经过点(0,
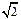 )且斜率为k的直线l与曲线W有两个不同的交点P和Q,求k的取值范围;
)且斜率为k的直线l与曲线W有两个不同的交点P和Q,求k的取值范围;(Ⅲ)已知点M(
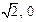 ),N(0, 1),在(Ⅱ)的条件下,是否存在常数k,使得向量
),N(0, 1),在(Ⅱ)的条件下,是否存在常数k,使得向量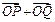 与
与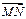 共线?如果存在,求出k的值;如果不存在,请说明理由.
共线?如果存在,求出k的值;如果不存在,请说明理由.(1) ;(2)
;(2)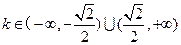 且
且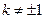 ;(3)不存在常数k,使得向量
;(3)不存在常数k,使得向量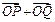 与
与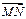 共线.
共线.
 ;(2)
;(2)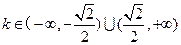 且
且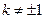 ;(3)不存在常数k,使得向量
;(3)不存在常数k,使得向量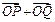 与
与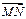 共线.
共线.(Ⅰ) 设C(x, y), ∵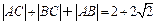 ,
, 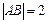 , ∴
, ∴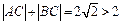 ,∴由定义知,动点C的轨迹是以A、B为焦点,长轴长为
,∴由定义知,动点C的轨迹是以A、B为焦点,长轴长为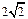 的椭圆除去与x轴的两个交点.
的椭圆除去与x轴的两个交点.
∴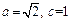 . ∴
. ∴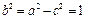 .∴W:
.∴W: 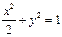
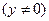 .……2分
.……2分
(Ⅱ) 设直线l的方程为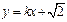 ,代入椭圆方程,得
,代入椭圆方程,得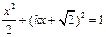 .
.
整理,得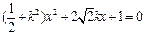 . ①…………………………5分
. ①…………………………5分
因为直线l与椭圆有两个不同的交点P和Q等价于
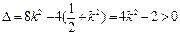 ,解得
,解得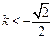 或
或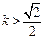 .
.
∴满足条件的k的取值范围为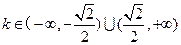 且
且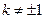 ……7分
……7分
(Ⅲ)设P(x1,y1),Q(x2,y2),则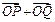 =(x1+x2,y1+y2),
=(x1+x2,y1+y2),
由①得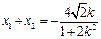 .② 又
.② 又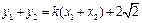 ③
③
因为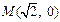 ,
,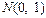 ,所以
,所以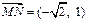 .………………………11分
.………………………11分
所以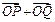 与
与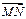 共线等价于
共线等价于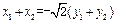 .将②③代入上式
.将②③代入上式
解得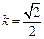 .所以不存在常数k,使得向量
.所以不存在常数k,使得向量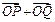 与
与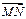 共线.…12分∴由定义知,动点C的轨迹是以A、B为焦点,长轴长为
共线.…12分∴由定义知,动点C的轨迹是以A、B为焦点,长轴长为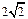 的椭圆除去与x轴的两个交点.
的椭圆除去与x轴的两个交点.
∴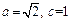 . ∴
. ∴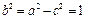 .∴W:
.∴W: 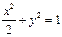
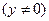 .……2分
.……2分
(Ⅱ) 设直线l的方程为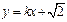 ,代入椭圆方程,得
,代入椭圆方程,得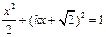 .
.
整理,得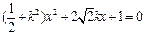 . ①…………………………5分
. ①…………………………5分
因为直线l与椭圆有两个不同的交点P和Q等价于
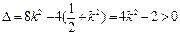 ,解得
,解得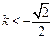 或
或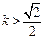 .
.
∴满足条件的k的取值范围为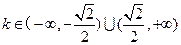 且
且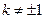 ……7分
……7分
(Ⅲ)设P(x1,y1),Q(x2,y2),则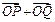 =(x1+x2,y1+y2),
=(x1+x2,y1+y2),
由①得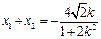 .② 又
.② 又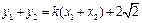 ③
③
因为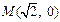 ,
,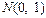 ,所以
,所以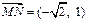 .………………………11分
.………………………11分
所以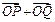 与
与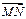 共线等价于
共线等价于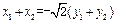 .将②③代入上式
.将②③代入上式
解得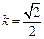 .所以不存在常数k,使得向量
.所以不存在常数k,使得向量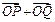 与
与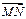 共线.…12分
共线.…12分
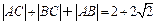 ,
, 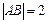 , ∴
, ∴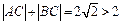 ,∴由定义知,动点C的轨迹是以A、B为焦点,长轴长为
,∴由定义知,动点C的轨迹是以A、B为焦点,长轴长为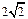 的椭圆除去与x轴的两个交点.
的椭圆除去与x轴的两个交点.∴
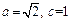 . ∴
. ∴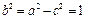 .∴W:
.∴W: 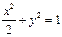
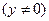 .……2分
.……2分(Ⅱ) 设直线l的方程为
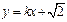 ,代入椭圆方程,得
,代入椭圆方程,得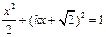 .
.整理,得
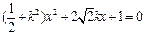 . ①…………………………5分
. ①…………………………5分因为直线l与椭圆有两个不同的交点P和Q等价于
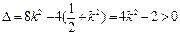 ,解得
,解得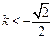 或
或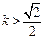 .
.∴满足条件的k的取值范围为
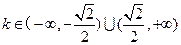 且
且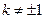 ……7分
……7分(Ⅲ)设P(x1,y1),Q(x2,y2),则
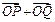 =(x1+x2,y1+y2),
=(x1+x2,y1+y2),由①得
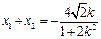 .② 又
.② 又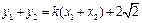 ③
③因为
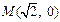 ,
,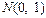 ,所以
,所以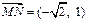 .………………………11分
.………………………11分所以
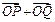 与
与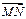 共线等价于
共线等价于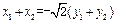 .将②③代入上式
.将②③代入上式解得
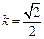 .所以不存在常数k,使得向量
.所以不存在常数k,使得向量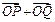 与
与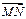 共线.…12分∴由定义知,动点C的轨迹是以A、B为焦点,长轴长为
共线.…12分∴由定义知,动点C的轨迹是以A、B为焦点,长轴长为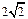 的椭圆除去与x轴的两个交点.
的椭圆除去与x轴的两个交点.∴
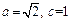 . ∴
. ∴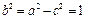 .∴W:
.∴W: 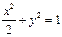
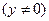 .……2分
.……2分(Ⅱ) 设直线l的方程为
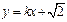 ,代入椭圆方程,得
,代入椭圆方程,得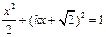 .
.整理,得
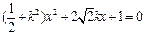 . ①…………………………5分
. ①…………………………5分因为直线l与椭圆有两个不同的交点P和Q等价于
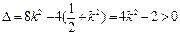 ,解得
,解得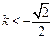 或
或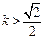 .
.∴满足条件的k的取值范围为
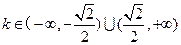 且
且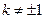 ……7分
……7分(Ⅲ)设P(x1,y1),Q(x2,y2),则
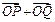 =(x1+x2,y1+y2),
=(x1+x2,y1+y2),由①得
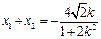 .② 又
.② 又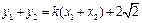 ③
③因为
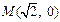 ,
,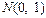 ,所以
,所以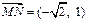 .………………………11分
.………………………11分所以
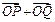 与
与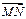 共线等价于
共线等价于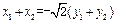 .将②③代入上式
.将②③代入上式解得
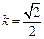 .所以不存在常数k,使得向量
.所以不存在常数k,使得向量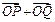 与
与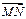 共线.…12分
共线.…12分
练习册系列答案
相关题目
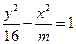 的离心率e=2,则m=____.
的离心率e=2,则m=____.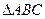 中,
中,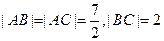 ,以
,以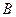 、
、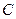 为焦点的椭圆恰好过
为焦点的椭圆恰好过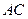 的中点
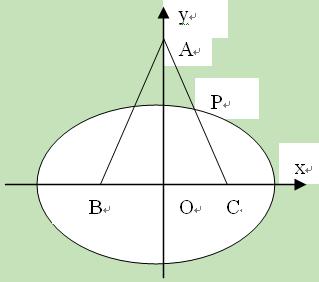
的中点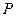 。
。
 作直线
作直线 与圆
与圆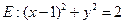 相交于
相交于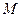 、
、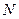 两点,试探究点
两点,试探究点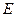 分割成弧长比值为
分割成弧长比值为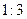 的两段弧吗?若能,求出直线
的两段弧吗?若能,求出直线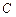 :
: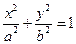
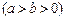 上的一动点
上的一动点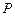 到右焦点的最短距离为
到右焦点的最短距离为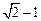 ,且右焦点到右准线的距离等于短半轴的长.
,且右焦点到右准线的距离等于短半轴的长.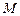 (
(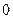 ,
,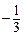 )的动直线
)的动直线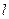 交椭圆
交椭圆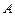 、
、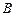 两点,试问:在坐标平面上是否存在一个定点
两点,试问:在坐标平面上是否存在一个定点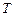 ,使得无论
,使得无论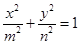 (
(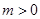 ,
,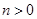 )的右焦点与抛物线
)的右焦点与抛物线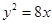 的焦点相同,离心率为
的焦点相同,离心率为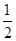 ,则此椭圆的方程为 ( )
,则此椭圆的方程为 ( )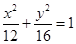
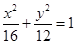
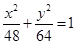
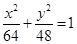
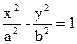 (a>0,b>0)上,C的焦距为4,则它的离心率为______
(a>0,b>0)上,C的焦距为4,则它的离心率为______ _______.
_______.
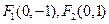 ,一条准线为
,一条准线为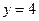 的椭圆上,且
的椭圆上,且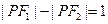 ,
,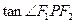 ____________。
____________。
 与抛物线
与抛物线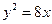 有 一个公共的焦点
有 一个公共的焦点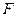 ,且两曲线的一个交点为
,且两曲线的一个交点为 ,若
,若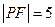 ,则双曲线方程为 .
,则双曲线方程为 .