题目内容
4.下列关于叙述错误的是( )| A. | 在△ABC中,a:b:c=sinA:sinB:sinC | |
| B. | 在△ABC中,a=b⇒sin2A=sin2B | |
| C. | 在△ABC中,余弦值较小的角所对的边也较小 | |
| D. | 在△ABC中,$\frac{a}{sinA}=\frac{a+b-c}{sinB-sinC+sinA}$ |
分析 在△ABC中,由正弦定理可得 a=2rsinA,b=2rsingB,c=2rsinC,结合大边对大角,判断各个选项是否成立,从而得出结论.
解答 解:在△ABC中,由正弦定理可得 a=2rsinA,b=2rsingB,c=2rsinC,
故有a:b:c=sinA:sinB:sinC,故A成立.
故有a=b,等价于sinA=sinB,且A,B为锐角,可得cosA=cosB,从而可求B成立.
余弦值为负数的角为钝角,根据大边对大角,可得C错误.
再根据比例式的性质可得D成立.
故选:C.
点评 本题主要了考查了正弦定理的应用,比例式的性质,大边对大角等知识的应用,属于基础题.

练习册系列答案
相关题目
12.已知菱形ABCD的边长为a,∠ABC=120°,则$\overrightarrow{BD}$•$\overrightarrow{CD}$=( )
| A. | -$\frac{1}{2}$a2 | B. | -$\frac{3}{2}$a2 | C. | $\frac{1}{2}$a2 | D. | $\frac{3}{2}$a2 |
13.在△ABC中,AB=2,BC=2.5,∠ABC=120°,若使△ABC绕直线BC旋转一周,则所形成的几何体的体积是( )
| A. | $\frac{9π}{2}$ | B. | $\frac{7π}{2}$ | C. | $\frac{5π}{2}$ | D. | $\frac{3π}{2}$ |
10.已知-2,a1,a2,-8成等差数列,-2,b,-8成等比数列,则$\frac{{a}_{2}-{a}_{1}}{b}$等于( )
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$或-$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
9.已知函数f(x)=sinx-$\frac{1}{{2{x^2}}}$,若$\frac{π}{3}<a<b<\frac{5π}{6}$,则( )
| A. | f(a)>f(b) | B. | f(a)<f(b) | C. | f(a)=f(b) | D. | f(a)f(b)>0 |
14.已知锐角α终边经过点P(cos50°,1+sin50°).则锐角α等于( )
| A. | 10° | B. | 20° | C. | 70° | D. | 80° |
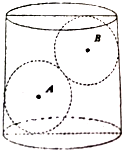 如图,在水平放置的直径与高相等的圆柱内,放入两个半径相等的小球(球A和球B),圆柱的底面直径为2+$\sqrt{2}$,向圆柱内注满水,水面刚好淹没小球B
如图,在水平放置的直径与高相等的圆柱内,放入两个半径相等的小球(球A和球B),圆柱的底面直径为2+$\sqrt{2}$,向圆柱内注满水,水面刚好淹没小球B