题目内容

10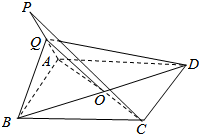．P是平行四边形ABCD所在平面外一点，Q是PA中点，对角线AC与BD相交于点O，求证：PC∥平面BDQ．

分析 由Q是PA中点，O为AC的中点，可证QO∥PC，即可证明PC∥平面BDQ．

解答 证明：∵Q是PA中点，对角线AC与BD相交于点O，四边形ABCD是平行四边形，
∴△PAC中，QO为中位线，QO∥PC，
∵P是平行四边形ABCD所在平面外一点，PC?平面QBD，OQ?平面BDQ．
∴PC∥平面BDQ．

点评 本题主要考查了直线与平面平行的判定，考查了推理论证能力和空间想象能力，属于基本知识的考查．

练习册系列答案
相关题目
20．已知集合M={3，m}，P={x|x2≤2x，x∈N}，M∩P={1}，又S=M∪P，则集合S的子集共有（　　）
A．16个B．8个C．7个D．3个
1．已知$\overrightarrow{a}$，$\overrightarrow{b}$均是非零向量，设$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为θ，是否存在这样的θ，使|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{3}$|$\overrightarrow{a}$-$\overrightarrow{b}$|成立？，若存在，求θ的值，若不存在，请说明理由．
18．已知函数f（x）满足下列关系式：（i）对于任意的x，y∈R，恒有2f（x）f（y）=f（$\frac{π}{2}$-x+y）-f（$\frac{π}{2}$-x-y）；（ii）f（$\frac{π}{2}$）=1．求证：
（1）f（0）=0；
（2）f（x）为奇函数；
（3）f（x）是以2π为周期的周期函数．
5．已知函数f（n）对任意的m，n∈N*，都有f（m+n）=f（m）+f（n）+2（m+n）+1，且f（1）=1
（1）若n∈N*，试求f（n）的表达式；
（2）若对于n∈N*且n≥2时，不等式f（n）≥（a+7）n-（a+10）恒成立，求实数a的取值范围．
15．设f（x）=2x2+bx+c，已知不等式f（x）＜0的解集是（0，5）
（1）求f（x）的解析式；
（2）若对于任意x∈[1，3]，不等式f（x）-tx≤-8有解，求实数t的取值范围．
2．下列方程所表示的曲线关于x轴对称的是（1）（2）（4）（5），关于x，y轴都对称的是（1）（2）（4）（5），关于原点对称的是（1）（2）（4）（5）．
（1）3x2+8y2=20
（2）x2-$\frac{{y}^{2}}{3}$=1
（3）x2+2y=0
（4）|x|+|y|=1
（5）$\sqrt{{x}^{2}+（y+3）^{2}}$+$\sqrt{{x}^{2}+（y-3）^{2}}$=10．
19．分解因式（x2+3x-2）（x2+3x+4）-16=（x2+3x+6）（x+4）（x-1）．
20．若集合A={x||x|＞1，x∈R}，B={y|y=2x2，x∈R}，则（∁RA）∩B=（　　）
A．{x|-1≤x≤1}B．{x|x≥0}C．{x|0≤x≤1}D．∅

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网