题目内容
2.下列方程所表示的曲线关于x轴对称的是(1)(2)(4)(5),关于x,y轴都对称的是(1)(2)(4)(5),关于原点对称的是(1)(2)(4)(5).(1)3x2+8y2=20
(2)x2-$\frac{{y}^{2}}{3}$=1
(3)x2+2y=0
(4)|x|+|y|=1
(5)$\sqrt{{x}^{2}+(y+3)^{2}}$+$\sqrt{{x}^{2}+(y-3)^{2}}$=10.
分析 直接利用曲线方程的对称性写出结果即可.
解答 解:(1)3x2+8y2=20,是椭圆方程,椭圆关于原点,坐标轴对称.
(2)x2-$\frac{{y}^{2}}{3}$=1,曲线是双曲线方程,关于原点,坐标轴对称.
(3)x2+2y=0,曲线是抛物线方程,开口向下,对称性为y轴,
(4)|x|+|y|=1,曲线是正方体,关于原点,坐标轴对称.
(5)$\sqrt{{x}^{2}+(y+3)^{2}}$+$\sqrt{{x}^{2}+(y-3)^{2}}$=10.满足焦点在y轴的椭圆,关于原点,坐标轴对称.
故答案为:(1)(2)(4)(5);
(1)(2)(4)(5);
(1)(2)(4)(5).
点评 本题考查曲线与方程的对称性,椭圆以及思想抛物线的阶段性的应用,是基础题.

练习册系列答案
相关题目
13.如图是一个算法的程序框图,若输入的x的值为2,则输出的y的值是( )
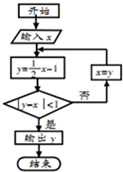

| A. | 0 | B. | -1 | C. | -$\frac{3}{2}$ | D. | -$\frac{7}{4}$ |
17.不等式(x+1)(2-x)>0的解集是( )
| A. | (-∞,-2)∪(-1,+∞) | B. | (-2,1) | C. | (-∞,-1)∪(2,+∞) | D. | (-1,2) |
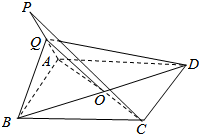 P是平行四边形ABCD所在平面外一点,Q是PA中点,对角线AC与BD相交于点O,求证:PC∥平面BDQ.
P是平行四边形ABCD所在平面外一点,Q是PA中点,对角线AC与BD相交于点O,求证:PC∥平面BDQ.