题目内容
18.已知函数f(x)满足下列关系式:(i)对于任意的x,y∈R,恒有2f(x)f(y)=f($\frac{π}{2}$-x+y)-f($\frac{π}{2}$-x-y);(ii)f($\frac{π}{2}$)=1.求证:(1)f(0)=0;
(2)f(x)为奇函数;
(3)f(x)是以2π为周期的周期函数.
分析 (1)令x=y=0,即可得到f(0)=0;
(2)令x=$\frac{π}{2}$,结合函数奇偶性的定义即可判断f(x)为奇函数;
(3)利用赋值法结合函数的周期性即可证明f(x)是以2π为周期的周期函数.
解答 解:(1)∵2f(x)f(y)=f($\frac{π}{2}$-x+y)-f($\frac{π}{2}$-x-y),
∴令x=y=0,代人2f(0)f(0)=f($\frac{π}{2}$)-f($\frac{π}{2}$)=0,
即得f(0)=0.
(2)对于任意的x,y∈R,
令x=$\frac{π}{2}$,带入2f(x)f(y)=f($\frac{π}{2}$-x+y)-f($\frac{π}{2}$-x-y),
得2f($\frac{π}{2}$)f(y)=f($\frac{π}{2}$-$\frac{π}{2}$+y)-f($\frac{π}{2}$-$\frac{π}{2}$-y),
即2f($\frac{π}{2}$)f(y)=f(y)-f(-y),
∵f($\frac{π}{2}$)=1,
∴2f(y)=f(y)-f(-y),
即 f(y)=-f(-y),
则f(-y)=-f(y),
即f(-x)=-f(x),则函数为奇函数.
(3)令x=0,y=$\frac{π}{2}$,
由2f(x)f(y)=f($\frac{π}{2}$-x+y)-f($\frac{π}{2}$-x-y),
得2f(0)f($\frac{π}{2}$)=f($\frac{π}{2}$+$\frac{π}{2}$)-f($\frac{π}{2}$-$\frac{π}{2}$),
即2f(0)f($\frac{π}{2}$)=f(π)-f(0),
即f(π)=0,
令x=π,y=a+$\frac{3π}{2}$ 代回2f(x)f(y)=f($\frac{π}{2}$-x+y)-f($\frac{π}{2}$-x-y),
得2f(π)f(a+$\frac{3π}{2}$)=f($\frac{π}{2}$-π+a+$\frac{3π}{2}$)-f($\frac{π}{2}$-π-a-$\frac{3π}{2}$),
即0=f(π+a)-f(-a),
即f(π+a)=f(-a),
则f(a+2π)=-f(π+a)=f(a),
即f(x+2π)=f(x),
则函数的周期T=2π.
点评 本题主要考查抽象函数的应用,利用赋值法是解决本题的关键.结合函数奇偶性和周期性的定义,进行转化,考查学生的转化能力.

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
| A. | 0 | B. | -1 | C. | -$\frac{3}{2}$ | D. | -$\frac{7}{4}$ |
| A. | ±3 | B. | ±5 | C. | 3或5 | D. | ±3或±5 |
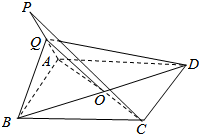 P是平行四边形ABCD所在平面外一点,Q是PA中点,对角线AC与BD相交于点O,求证:PC∥平面BDQ.
P是平行四边形ABCD所在平面外一点,Q是PA中点,对角线AC与BD相交于点O,求证:PC∥平面BDQ.