题目内容
1.已知$\overrightarrow{a}$,$\overrightarrow{b}$均是非零向量,设$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为θ,是否存在这样的θ,使|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{3}$|$\overrightarrow{a}$-$\overrightarrow{b}$|成立?,若存在,求θ的值,若不存在,请说明理由.分析 假设存在这样的θ,使|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{3}$|$\overrightarrow{a}$-$\overrightarrow{b}$|成立,可得$\sqrt{{\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}+2\overrightarrow{a}•\overrightarrow{b}}$=$\sqrt{3}$$\sqrt{{\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}-2\overrightarrow{a}•\overrightarrow{b}}$,化简整理即可得出.
解答 解:假设存在这样的θ,使|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{3}$|$\overrightarrow{a}$-$\overrightarrow{b}$|成立,
∴$\sqrt{{\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}+2\overrightarrow{a}•\overrightarrow{b}}$=$\sqrt{3}$$\sqrt{{\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}-2\overrightarrow{a}•\overrightarrow{b}}$,
化为${\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}$-4$\overrightarrow{a}•\overrightarrow{b}$=0,
∴cosθ=$\frac{{\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}}{4|\overrightarrow{a}||\overrightarrow{b}|}$≥$\frac{2|\overrightarrow{a}||\overrightarrow{b}|}{4|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{1}{2}$,
∴θ∈$[0,\frac{π}{3}]$.
点评 本题考查了向量的数量积运算性质、向量夹角公式、三角函数的单调性,考查了推理能力与计算能力,属于中档题.

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
| A. | 0 | B. | -1 | C. | -$\frac{3}{2}$ | D. | -$\frac{7}{4}$ |
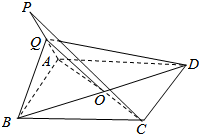 P是平行四边形ABCD所在平面外一点,Q是PA中点,对角线AC与BD相交于点O,求证:PC∥平面BDQ.
P是平行四边形ABCD所在平面外一点,Q是PA中点,对角线AC与BD相交于点O,求证:PC∥平面BDQ.