题目内容
一个动圆与定圆 :
: 相外切,且与定直线
相外切,且与定直线 :
: 相切,则此动圆的圆心
相切,则此动圆的圆心 的轨迹方程是( )
的轨迹方程是( )
A.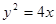 | B. | C. | D. |
D.
解析试题分析:由题意知,点 到定点
到定点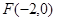 的距离减去1等于到定直线
的距离减去1等于到定直线 :
: 的距离,即点
的距离,即点 到定点
到定点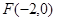 的距离等于到定直线
的距离等于到定直线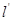 :
: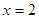 的距离.由抛物线的定义知,点
的距离.由抛物线的定义知,点 的轨迹方程为抛物线且焦点坐标为
的轨迹方程为抛物线且焦点坐标为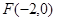 ,准线方程为
,准线方程为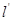 :
: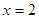 ,即可求出该点的轨迹方程.
,即可求出该点的轨迹方程.
考点:抛物线的定义;轨迹方程.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知抛物线 的准线与圆
的准线与圆 相切,则
相切,则 的值为
的值为
A. | B.1 | C.2 | D.4 |
设 ,
,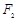 分别是椭圆
分别是椭圆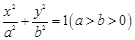 的左、右焦点,过
的左、右焦点,过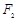 的直线交椭圆于
的直线交椭圆于 ,
, 两点,若
两点,若 ,
, ,则椭圆的离心率为( )
,则椭圆的离心率为( )
A. | B. | C. | D. |
已知曲线 :
: 和
和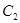 :
: ,且曲线
,且曲线 的焦点分别为
的焦点分别为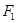 、
、 ,点
,点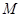 是
是 和
和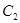 的一个交点,则△
的一个交点,则△ 的形状是( )
的形状是( )
| A.锐角三角形 | B.直角三角形 | C.钝角三角形 | D.都有可能 |
设抛物线x2=4y与椭圆 +
+ =1交于点E,F,则△OEF(O为坐标原点)的面积为( )
=1交于点E,F,则△OEF(O为坐标原点)的面积为( )
A.3 | B.4 | C.6 | D.12 |
 的焦点F,且交抛物线与A、B两点,若AB的中点到抛物线准线的距离1,则P的值为( ).
的焦点F,且交抛物线与A、B两点,若AB的中点到抛物线准线的距离1,则P的值为( ). C.
C. D.
D.





 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,且双曲线的离心率等于
的焦点重合,且双曲线的离心率等于 ,则该双曲线的方程为( )
,则该双曲线的方程为( )



 、
、 且圆心在x轴上的圆的标准方程并判断点
且圆心在x轴上的圆的标准方程并判断点 与圆的关系.
与圆的关系.