题目内容
10.公差不为零的等差数列{an}中,a1=10,a1,a3,a7成等比数列,则公差d=5.分析 a1,a3,a7成等比数列,可得${a}_{3}^{2}$=a1a7,代入化简解出即可.
解答 解:∵a1,a3,a7成等比数列,
∴${a}_{3}^{2}$=a1a7,
∴(10+2d)2=10(10+6d),d≠0,
则公差d=5.
故答案为:5.
点评 本题考查了等差数列的通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
20.已知函数y=$\frac{{\sqrt{1-x}}}{{{x^2}-4}}$,其定义域为( )
| A. | (-∞,1] | B. | (-∞,2] | C. | (-∞,-2)∪(-2,1] | D. | [1,2)∪(2,+∞) |
2.已知点A(-3,8),B(2,2),点P是x轴上的点,则当|AP|+|PB|最小时点P的坐标( )
| A. | (1,0) | B. | ($\frac{1}{2}$,0) | C. | ($\frac{1}{3}$,0) | D. | ($\frac{1}{4}$,0) |
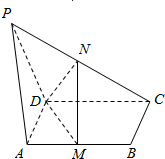 如图,PA⊥平面ABCD,ABCD是矩形,M、N分别是AB,PC的中点.
如图,PA⊥平面ABCD,ABCD是矩形,M、N分别是AB,PC的中点.