题目内容
19.已知1+sinθ$\sqrt{1-co{s}^{2}θ}+cosθ\sqrt{1-si{n}^{2}θ}$=0,则θ的取值范围是[2kπ+π,$2kπ+\frac{3π}{2}$],k∈Z,.分析 通过θ所在象限,化简表达式,求解即可.
解答 解:1+sinθ$\sqrt{1-co{s}^{2}θ}+cosθ\sqrt{1-si{n}^{2}θ}$=0,
可得1+sinθ|sinθ|+cosθ|cosθ|=0,
当θ∈[2kπ,$2kπ+\frac{π}{2}$],k∈Z,上式化为:1+sin2θ+cos2θ=0,等式不成立.
当θ∈[$2kπ+\frac{π}{2}$,2kπ+π],k∈Z,上式化为:1+sin2θ-cos2θ=0,可得cos2θ=1,2θ=2kπ,θ=kπ,
可得θ=2kπ+π,k∈Z等式成立.
当θ∈[2kπ+π,$2kπ+\frac{3π}{2}$],k∈Z,上式化为:1-sin2θ-cos2θ=0,等式恒成立.
当θ∈[$2kπ+\frac{3π}{2}$,2kπ+2π],k∈Z,上式化为:1-sin2θ+cos2θ=0,cos2θ=-1,2θ=2kπ+π,θ=kπ+$\frac{π}{2}$舍去.
综上:θ∈[2kπ+π,$2kπ+\frac{3π}{2}$],k∈Z,
故答案为:[2kπ+π,$2kπ+\frac{3π}{2}$],k∈Z,
点评 本题考查三角函数的化简求值,考查计算能力.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
9.已知函数f(x)=$\left\{\begin{array}{l}{ln(1-x)}&{x≤0}\\{-{x}^{2}-2x}&{x>0}\end{array}\right.$,若|f(x)|≥ax,则a的取值范围是( )
| A. | [0,+∞) | B. | [1,+∞) | C. | [-1,2] | D. | [0,2] |
11.若函数f(x)=$\left\{\begin{array}{l}{x+5}&{x<3}\\{2x-m}&{x≥3}\end{array}\right.$,且f(f(3))>6,则实数m的取值范围为( )
| A. | (3,5) | B. | (-∞,2)∪(2,3) | C. | (2,3) | D. | (-∞,2)∪(3,5) |
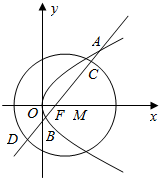 如图,抛物线C1:y2=2px(p>0)和圆C2:(x-1)2+y2=r2(r>0),M为圆C2的圆心,过抛物线C1的焦点F的直线y=k(x-$\frac{p}{2}$)与C1交于A,B两点,与圆C2交与C,D两点(点C在A,B之间)且△AOF的外心到抛物线C1的准线的距离为$\frac{3}{4}$.
如图,抛物线C1:y2=2px(p>0)和圆C2:(x-1)2+y2=r2(r>0),M为圆C2的圆心,过抛物线C1的焦点F的直线y=k(x-$\frac{p}{2}$)与C1交于A,B两点,与圆C2交与C,D两点(点C在A,B之间)且△AOF的外心到抛物线C1的准线的距离为$\frac{3}{4}$.