题目内容
19.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}-bx+c\\;x≥0}\\{{e}^{x}\\;x<0}\end{array}\right.$,其中b=$\frac{2}{π}$${∫}_{-2}^{2}$$\sqrt{4-{x}^{2}}$dx,c为目标函数z=2x+4y在约束条件$\left\{\begin{array}{l}{y≥0}\\{x+y-1≤0}\\{x-y+2≥0}\end{array}\right.$,内的最大值,则f(x)<10的解集为( )| A. | (-∞,0) | B. | [0,5) | C. | (-∞,5) | D. | (-∞,5] |
分析 根据积分的几何意义求出b,利用线性规划的知识求出c,利用分类讨论的思想解不等式即可.
解答 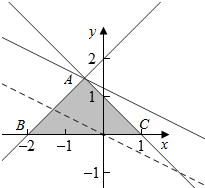 解:y=$\sqrt{4-{x}^{2}}$的轨迹是半径为2的上半圆,对应的面积S=$\frac{1}{2}π×{2}^{2}$=2π,
解:y=$\sqrt{4-{x}^{2}}$的轨迹是半径为2的上半圆,对应的面积S=$\frac{1}{2}π×{2}^{2}$=2π,
则b=$\frac{2}{π}$${∫}_{-2}^{2}$$\sqrt{4-{x}^{2}}$dx=$\frac{2}{π}$×2π=4,
作出不等式组对应的平面区域如图:
由z=2x+4y得y=-$\frac{1}{2}$x+$\frac{z}{4}$,
平移直线y=-$\frac{1}{2}$x+$\frac{z}{4}$,由图象可知当直线y=-$\frac{1}{2}$x+$\frac{z}{4}$经过点A时,
直线y=-$\frac{1}{2}$x+$\frac{z}{4}$的截距最大,此时z最大,
由$\left\{\begin{array}{l}{x+y-1=0}\\{x-y+2=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=-\frac{1}{2}}\\{y=\frac{3}{2}}\end{array}\right.$,即A(-$\frac{1}{2}$,$\frac{3}{2}$),
此时z=-$\frac{1}{2}$×2+$\frac{3}{2}$×4=-1+6=5,
即c=5,
则f(x)=$\left\{\begin{array}{l}{{x}^{2}-4x+5,}&{x≥0}\\{{e}^{x},}&{x<0}\end{array}\right.$,
若x≥0,由f(x)<10得f(x)=x2-4x+5<10,
即x2-4x-5<0,解得-1<x<5,此时0≤x<5,
若x<0,f(x)=ex<1,此时f(x)<10恒成立,
综上x<5,
故选:C
点评 本题主要考查不等式的求解涉及的内容包括积分的几何意义以及线性规划的知识,利用数形结合是解决本题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | 6+$\sqrt{3}$ | B. | 6-$\sqrt{3}$ | C. | 6+$\frac{\sqrt{42-24\sqrt{2}}}{2}$ | D. | 6-$\frac{\sqrt{42-24\sqrt{2}}}{2}$ |
| A. | .[-1,+∞) | B. | (-∞,-1] | C. | (1,+∞) | D. | .(-∞,1] |
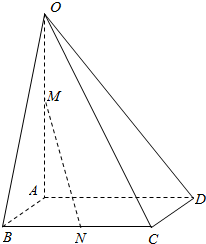 如图,在四棱锥O-ABCD中,底面ABCD为平行四边形,M为OA的中点,N为BC的中点,求证:MN∥平面OCD.
如图,在四棱锥O-ABCD中,底面ABCD为平行四边形,M为OA的中点,N为BC的中点,求证:MN∥平面OCD.