题目内容
7.设函数f(x)=log2($\sqrt{{x}^{2}+1}$+x)(1)求函数f(x)的定义域;
(2)判断函数f(x)的奇偶性;
(3)求证:函数f(x)在[0,+∞)上单调递增.
分析 (1)利用$\sqrt{{x}^{2}+1}$>|x|≥-x,可以$\sqrt{{x}^{2}+1}$+x>0恒成立,得出定义域,
(2)根据奇偶性定义证明.
(3)利用单调性定义证明,关键$\sqrt{{x}_{1}^{2}+1}$+x1$<\sqrt{{x}_{2}^{2}+1}$+x2,根据对数函数性质证明.
解答 解:函数f(x)=log2($\sqrt{{x}^{2}+1}$+x)
(1)$\sqrt{{x}^{2}+1}$+x>0
∵$\sqrt{{x}^{2}+1}$>|x|≥-x,
∴$\sqrt{{x}^{2}+1}$+x>0恒成立
函数f(x)的定义域:(-∞,+∞)
(2)∵f(-x)=log2($\sqrt{{x}^{2}+1}$-x)=-log2($\sqrt{{x}^{2}+1}$+x)=-f(x)
∴函数f(x)为奇函数;
(3)设任意实数x1,x2∈[0,+∞)且x1<x2,
∵$\sqrt{{x}_{1}^{2}+1}$+x1$<\sqrt{{x}_{2}^{2}+1}$+x2,
∴log2($\sqrt{{x}_{1}^{2}+1}$+x1)<log2($\sqrt{{x}_{2}^{2}+1}$+x2)
即f(x1)<f(x2)
∴函数f(x)在[0,+∞)上单调递增.
点评 本题考察了函数的性质,综合运用解决问题,属于中档题,关键是利用概念,不等式转化证明.

练习册系列答案
相关题目
17.若cos65°=a,则sin25°的值是( )
| A. | -a | B. | a | C. | $\sqrt{1-{a}^{2}}$ | D. | -$\sqrt{1-{a}^{2}}$ |
12.若函数$f(x)=-\frac{1}{2}{({x-2})^2}+alnx$在(1,+∞)上是减函数,则实数a的取值范围是( )
| A. | .[-1,+∞) | B. | (-∞,-1] | C. | (1,+∞) | D. | .(-∞,1] |
19.已知数列{an},其通项公式an=3n-18,则其前n项和Sn取最小值时n的值为( )
| A. | 4 | B. | 5或6 | C. | 6 | D. | 5 |
16.已知集合A={0,1,2,3,4,5},B={x|x2-7x+10<0},则A∩B的子集可以是( )
| A. | {3,4,5} | B. | {4,5} | C. | {3,5} | D. | {4} |
17.已知集合M={-1,0,1,2,3,4},N={-1,2,3,5},P=M∩N,则P的子集共有( )
| A. | 8个 | B. | 6个 | C. | 4个 | D. | 2个 |
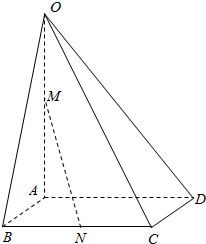 如图,在四棱锥O-ABCD中,底面ABCD为平行四边形,M为OA的中点,N为BC的中点,求证:MN∥平面OCD.
如图,在四棱锥O-ABCD中,底面ABCD为平行四边形,M为OA的中点,N为BC的中点,求证:MN∥平面OCD.