��Ŀ����
14�� ��֪��B����ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�����϶��㣬F1��F2�ֱ�����Բ�����ҽ��㣬ֱ��BF1��BF2����Բ�ֱ���E��F���㣬��BEFΪ�ȱ������Σ�
��֪��B����ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�����϶��㣬F1��F2�ֱ�����Բ�����ҽ��㣬ֱ��BF1��BF2����Բ�ֱ���E��F���㣬��BEFΪ�ȱ������Σ���1������ԲC�������ʣ�
��2����֪�㣨1��$\frac{3}{2}$������ԲC�ϣ���ֱ��l��y=kx+m����ԲC����M��N���㣬��ֱ��F1M��F2N����б�Ƿֱ�Ϊ�����£��Ҧ�+��=$\frac{��}{2}$����֤��ֱ��l�����㣬����ö�������꣮
���� ������������Ϊ�ȱ������Σ���ʽ��������ʣ�
�����������Բ���̣�ֱ��l��y=kx+m����ԲC�����������ԣ�k2-1��x1x2+��mk+1����x1+x2��+m2-1=0����������⣮
��� �⣺����B��0��b��F1��-c��0����F2��c��0����
�֡�BEFΪ�ȱ������Σ����ԣ���BF1F2Ϊ�ȱ������Σ�
��2c=$\sqrt{{b}^{2}+{c}^{2}}$������a2=b2+c2��
�ɢ٢ڽ��$e=\frac{c}{a}=\frac{1}{2}$
��ԲC��������$e=\frac{1}{2}$������3�֣�
������������Բ����Ϊ3x2+4y2=3a2�����ڵ㣨1��$\frac{3}{2}$������ԲC�ϣ�
���a2=4��b2=3�������Բ����Ϊ$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$������4�֣�
����$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\\{y=kx+m}\end{array}\right.$����ȥy���ã�3+4k2��x2+8mkx+4m2-12=0����M��x1��y1����N��x2��y2����
��${x}_{1}+{x}_{2}=\frac{-8km}{3+4{k}^{2}}��{x}_{1}{x}_{2}=\frac{4{m}^{2}-12}{3+4{k}^{2}}$����$��+��=\frac{��}{2}$����sin��=cos�£�cos��=sin�£�����7�֣�
���tan��tan��=1����${k}_{M{F}_{1}}{k}_{M{F}_{2}}=1$����ˣ�kx1+m����kx2+m��=��x1-1����x2-1����
���ԣ�k2-1��x1x2+��mk+1����x1+x2��+m2-1=0������9�֣�
���$��{k}^{2}-1��\frac{4{m}^{2}-12}{3+4{k}^{2}}+��mk+\sqrt{3}����\frac{-8mk}{3+4{k}^{2}}��$+m2-1=0����������
m2+8mk+16k2-9=0������m+4k��2=3��m=-4k��3������11�֣�
����ֱ�߷���Ϊy=k��x-4����3�����ֱ�߹����㣨4��3����4��-3��������13�֣�
���� ������Ҫ��������Բ�����ʵ���ֱ�ߺ�Բ���ߵ��ۺ�Ӧ�ã������е��⣬�߿������漰��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | $\sqrt{2}$ | B�� | $\sqrt{3}$ | C�� | 2 | D�� | $\sqrt{2}$+1 |
| A�� | -4 | B�� | 3 | C�� | 3��-4 | D�� | ��4 |
| A�� | x-y+2=0 | B�� | x+y+2=0 | C�� | x+y-2=0 | D�� | x-y-2=0 |
| A�� | ��-$\frac{3}{4}$��6�� | B�� | ��-6��$\frac{3}{4}$�� | C�� | ��-�ޣ�-6���ȣ�$\frac{3}{4}$��+�ޣ� | D�� | ��-�ޣ�-$\frac{3}{4}$���ȣ�6��+�ޣ� |
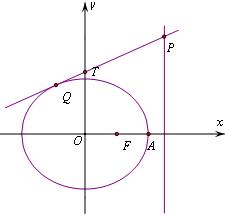 ��ͼ����֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������e=$\frac{1}{2}$���ҽ���ΪF���Ҷ���ΪA��PΪֱ��x=$\frac{5}{4}$a�ϵ�����һ�㣬�ң�$\overrightarrow{PF}$+$\overrightarrow{PA}$��•$\overrightarrow{AF}$=2��
��ͼ����֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������e=$\frac{1}{2}$���ҽ���ΪF���Ҷ���ΪA��PΪֱ��x=$\frac{5}{4}$a�ϵ�����һ�㣬�ң�$\overrightarrow{PF}$+$\overrightarrow{PA}$��•$\overrightarrow{AF}$=2�� ��ͼ����ֱ������ABC-A1B1C1�У�����Ϊ�ȱ������Σ�DΪAC���е㣬AA1=AB=6��
��ͼ����ֱ������ABC-A1B1C1�У�����Ϊ�ȱ������Σ�DΪAC���е㣬AA1=AB=6��