题目内容
3．已知函数f（x）=2ln x-xf′（1），则曲线y=f（x）在x=1处的切线方程是（ ）| A． | x-y+2=0 | B． | x+y+2=0 | C． | x+y-2=0 | D． | x-y-2=0 |
分析 求出f′（x），由题意可知曲线在点（1，f（1））处的切线方程的斜率等于f′（1），所以把x=1代入到f′（x）中即可求出f′（1）的值，得到切线的斜率，然后把x=1和f′（1）的值代入到f（x）中求出切点的纵坐标，根据切点坐标和斜率直线切线的方程即可．
解答 解：f′（x）=2ln x-xf′（1），
由题意可知，曲线在（1，f（1））处切线方程的斜率k=f′（1），
则f′（1）=2-f′（1），解得f′（1）=1，
则f（1）=-1，所以切点（1，-1）
所以切线方程为：y+1=x-1，化简得x-y-2=0
故选：D．
点评 此题考查学生会利用导数求过曲线上某点切线方程的斜率，会根据一点和斜率写出直线的方程，是一道中档题．
练习册系列答案
智趣暑假温故知新系列答案
相关题目
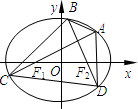如图，在平面直角坐标系xOy中，四边形ABCD的顶点都在椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上，对角线AC与BD分别过椭圆的左焦点F1（-1，0）和右焦点F2（1，0），且AC⊥BD，椭圆的一条准线方程为x=4．
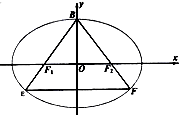已知点B是椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的上顶点，F1，F2分别是椭圆的左右焦点，直线BF1，BF2与椭圆分别交于E，F两点，△BEF为等边三角形．
18．在等比数列{an}中，a1=5，q=1，则S6=（ ）
| A． | 5 | B． | 0 | C． | 不存在 | D． | 30 |