题目内容
19.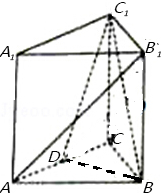 如图,在直三棱柱ABC-A1B1C1中,底面为等边三角形,D为AC的中点,AA1=AB=6.
如图,在直三棱柱ABC-A1B1C1中,底面为等边三角形,D为AC的中点,AA1=AB=6.(Ⅰ)求证:直线AB1∥平面BC1D;
(Ⅱ)求证:平面BC1D⊥平面ACC1A;
(Ⅲ)求三棱锥C-BC1D的体积.
分析 (Ⅰ)连接B1C交BC1于点O,连接OD,则点O为B1C的中点,证明:A1B∥OD,即可证明直线AB1∥平面BC1D;
(Ⅱ)证明BD⊥平面ACC1A1,即可证明:平面BC1D⊥平面ACC1A;
(Ⅲ)利用${V}_{C-B{C}_{1}D}$=${V}_{{C}_{1}-BCD}$,求三棱锥C-BC1D的体积.
解答  (Ⅰ)证明:连接B1C交BC1于点O,连接OD,则点O为B1C的中点.
(Ⅰ)证明:连接B1C交BC1于点O,连接OD,则点O为B1C的中点.
∵D为AC中点,得DO为△AB1C中位线,
∴A1B∥OD.
∵OD?平面AB1C,A1B?平面AB1C,
∴直线AB1∥平面BC1D;…(4分)
(Ⅱ) 证明:∵AA1⊥底面ABC,∴AA1⊥BD,
∵底面ABC正三角形,D是AC的中点,
∴BD⊥AC
∵AA1∩AC=A,∴BD⊥平面ACC1A1,
∵BD?平面BC1D,∴平面 BC1D⊥平面ACC1A;…(8分)
(Ⅲ)解:由(Ⅱ)知,△ABC中,BD⊥AC,BD=BCsin60°=3$\sqrt{3}$
∴S△BCD=$\frac{1}{2}×3×3\sqrt{3}$=$\frac{9\sqrt{3}}{2}$,
∴${V}_{C-B{C}_{1}D}$=${V}_{{C}_{1}-BCD}$=$\frac{1}{3}•\frac{9\sqrt{3}}{2}•6$=9$\sqrt{3}$. …(12分)
点评 本题考查线面平行,平面与平面垂足,考查三棱锥体积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
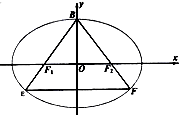 已知点B是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的上顶点,F1,F2分别是椭圆的左右焦点,直线BF1,BF2与椭圆分别交于E,F两点,△BEF为等边三角形.
已知点B是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的上顶点,F1,F2分别是椭圆的左右焦点,直线BF1,BF2与椭圆分别交于E,F两点,△BEF为等边三角形.