题目内容
【题目】已知函数![]() .
.
(1)当a=![]() 时,试判断函数f(x)的单调性;
时,试判断函数f(x)的单调性;
(2)设g(x)=![]() ,若g(x)有唯一零点,求实数a的取值范围.
,若g(x)有唯一零点,求实数a的取值范围.
【答案】(1)f(x)在(0,+∞)上单调递减.(2)![]() .
.
【解析】
(1)求出![]() ,两次求导,可判断在区间
,两次求导,可判断在区间![]()
![]() 恒成立,从而可得结果;(2)g(x)=
恒成立,从而可得结果;(2)g(x)=![]() ,x>0,g(x)=
,x>0,g(x)=![]() +2ax,分四种情况讨论,分别利用导数研究函数的单调性,求出函数的极值,结合单调性与极值分别判断是否符合题意,从而得到实数a的取值范围.
+2ax,分四种情况讨论,分别利用导数研究函数的单调性,求出函数的极值,结合单调性与极值分别判断是否符合题意,从而得到实数a的取值范围.
(1)当a=![]() 时,f(x)=
时,f(x)=![]() ,x>0,
,x>0,
求导得![]() ,令p(x)=
,令p(x)=![]() ,则p(x)=
,则p(x)=![]() ,
,
当x>1时,p(x)<0,当0<x<1时,p(x)>0,
所以f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
所以f(x)≤f(1)=0,当且仅当x=1时,等号成立,
所以f(x)在(0,+∞)上单调递减.
(2)g(x)=![]() ,x>0,g(x)=
,x>0,g(x)=![]() +2ax,
+2ax,
①当a≥0时,g(x)>0,g(x)在(0,+∞)上单调递增,
因为g(1)=0,所以g(x)有唯一零点.
②当a=![]() 时,g(x)=
时,g(x)=![]() ,
,
当0<x<1时,g(x)>0,当x>1时,g(x)<0,
则g(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
因为g(1)=0,所以g
③当![]() <a<0时,由g(x)=0,得x=
<a<0时,由g(x)=0,得x=![]() >1,
>1,
当0<x<![]() 时,g(x)>0,当x>
时,g(x)>0,当x>![]() 时,g(x)<0,
时,g(x)<0,
则g(x)在(0,![]() )上单调递增,在(
)上单调递增,在(![]() ,+∞)上单调递减,
,+∞)上单调递减,
因为g(1)=0,所以g(![]() )>0,
)>0,
由(1)可知,lnx≤![]() ,当且仅当x=1时等号成立,
,当且仅当x=1时等号成立,
因为![]() >
>![]() >1(注:因为
>1(注:因为![]() <a<0,所以
<a<0,所以![]() ,所以
,所以![]() ,所以
,所以![]() ,因为
,因为![]() ,所以
,所以![]() ,所以
,所以![]() >
>![]() >1),
>1),
且![]() ,
,
所以g(x)在(![]() ,
,![]() )上存在一个零点,
)上存在一个零点,
即g(x)存在两个零点,不符合题意.
④当a<![]() 时,由g(x)=0,得x=
时,由g(x)=0,得x=![]() <1,
<1,
当0<x<![]() 时,g(x)>0,当x>
时,g(x)>0,当x>![]() 时,g(x)<0,
时,g(x)<0,
则g(x)在(0,![]() )上单调递增,在(
)上单调递增,在(![]() ,+∞)上单调递减,
,+∞)上单调递减,
因为g(1)=0,所以g(![]() )>0,
)>0,
令h(x)=xex+1,h(x)=(x+1)ex,
易知h(x)在![]() 上单调递减,则在
上单调递减,则在![]() 上h(x)>
上h(x)>![]() =1-
=1-![]() >0.
>0.
因为a<![]() ,所以2a<
,所以2a<![]() ,所以h(2a)=2ae2a+1>0,即ea<
,所以h(2a)=2ae2a+1>0,即ea<![]() <1,
<1,
此时g(ea)=![]() =ae2a<0,
=ae2a<0,
所以g(x)在(ea,![]() )上存在一个零点,且g(1)=0,
)上存在一个零点,且g(1)=0,
即g(x)存在两个零点,不符合题意.
综上所述,若g(x)有唯一零点,则实数a的取值范围是![]() .
.

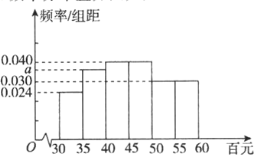
【题目】某省数学学会为选拔一批学生代表该省参加全国高中数学联赛,在省内组织了一次预选赛,该省各校学生均可报名参加.现从所有参赛学生中随机抽取![]() 人的成绩进行统计,发现这
人的成绩进行统计,发现这![]() 名学生中本次预选赛成绩优秀的男、女生人数之比为
名学生中本次预选赛成绩优秀的男、女生人数之比为![]() ,成绩一般的男、女生人数之比为
,成绩一般的男、女生人数之比为![]() .已知从这
.已知从这![]() 名学生中随机抽取一名学生,抽到男生的概率是
名学生中随机抽取一名学生,抽到男生的概率是![]()
(1)请将下表补充完整,并判断是否有![]() 的把握认为在本次预选赛中学生的成绩优秀与性别有关?
的把握认为在本次预选赛中学生的成绩优秀与性别有关?
成绩优秀 | 成绩一般 | 总计 | |
男生 | |||
女生 | |||
总计 |
|
(2)以样本估计总体,视样本频率为相应事件发生的概率,从所有本次预选赛成绩优秀的学生中随机抽取![]() 人代表该省参加全国联赛,记抽到的女生人数为
人代表该省参加全国联赛,记抽到的女生人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式: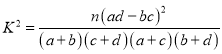 ,其中
,其中![]() ;
;
临界值表供参考:
|
|
|
|
|
|
|
|
|
|
|
|