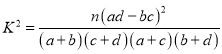��Ŀ����
����Ŀ��ijʡ��ѧѧ��Ϊѡ��һ��ѧ��������ʡ�μ�ȫ��������ѧ��������ʡ����֯��һ��Ԥѡ������ʡ��Уѧ�����ɱ����μ�.�ִ����в���ѧ���������ȡ![]() �˵ijɼ�����ͳ�ƣ�������
�˵ijɼ�����ͳ�ƣ�������![]() ��ѧ���б���Ԥѡ���ɼ�������С�Ů������֮��Ϊ
��ѧ���б���Ԥѡ���ɼ�������С�Ů������֮��Ϊ![]() ���ɼ�һ����С�Ů������֮��Ϊ
���ɼ�һ����С�Ů������֮��Ϊ![]() .��֪����
.��֪����![]() ��ѧ���������ȡһ��ѧ�����鵽�����ĸ�����
��ѧ���������ȡһ��ѧ�����鵽�����ĸ�����![]()
��1���뽫�±��������������ж��Ƿ���![]() �İ�����Ϊ�ڱ���Ԥѡ����ѧ���ijɼ��������Ա��йأ�
�İ�����Ϊ�ڱ���Ԥѡ����ѧ���ijɼ��������Ա��йأ�
�ɼ����� | �ɼ�һ�� | �ܼ� | |
���� | |||
�� | |||
�ܼ� |
|
��2���������������壬������Ƶ��Ϊ��Ӧ�¼������ĸ��ʣ������б���Ԥѡ���ɼ������ѧ���������ȡ![]() �˴�����ʡ�μ�ȫ���������dz鵽��Ů������Ϊ
�˴�����ʡ�μ�ȫ���������dz鵽��Ů������Ϊ![]() �����������
�����������![]() �ķֲ��м���ѧ����.
�ķֲ��м���ѧ����.
�ο���ʽ��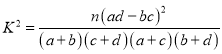 ������
������![]() ��
��
�ٽ�ֵ�����ο���
|
|
|
|
|
|
|
|
|
|
|
|
���𰸡���1�����������,��![]() �İ�����Ϊ�����йأ���2���������
�İ�����Ϊ�����йأ���2���������
��������
(1)����֪���ʺͱ������������������ж����Լ���ý⣻
(2)����������Ӷ���ֲ������ݶ���ֲ�����������ֵ���.
��������1�����ݱ����������ݼ���ɵã�
�ɼ����� | �ɼ�һ�� | �ܼ� | |
���� |
|
|
|
�� |
|
|
|
�ܼ� |
|
|
|
![]() ��
��
����![]() �İ�����Ϊ�����йأ�
�İ�����Ϊ�����йأ�
��2������֪![]() ����
����![]() �ķֲ���Ϊ��
�ķֲ���Ϊ��
|
|
|
|
|
|
|
|
|
|
![]() .
.

����Ŀ��ij�е��������ij���ù������ŵ�·�����������110��������·�Ľ�ͨ�����߶Կ�Խ�������߹������ŵĿ������õ�������������
�� | Ů | �ϼ� | |
�߹������� | 40 | 20 | 60 |
��Խ���� | 20 | 30 | 50 |
�ϼ� | 60 | 50 | 110 |
����![]() .
.
| 0.050 | 0.010 | 0.001 |
K | 3.841 | 6.635 | 10.828 |
����Եõ���ȷ�Ľ�����( )
A.��99%���ϵİ�����Ϊ��ѡ�����·�ķ�ʽ���Ա��йء�
B.��99%���ϵİ�����Ϊ��ѡ�����·�ķ�ʽ���Ա��ء�
C.�ڷ�����ĸ��ʲ�����0.1%��ǰ���£���Ϊ��ѡ�����·�ķ�ʽ���Ա��йء�
D.�ڷ�����ĸ��ʲ�����0.1%��ǰ���£���Ϊ��ѡ�����·�ķ�ʽ���Ա��ء�
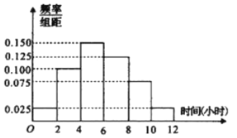
����Ŀ��������ʵʩ��Ȼ���۸�����ƣ�����ǰ�����������Ȼ���۸�����Ƶ�̬�ȣ���������![]() �������ֽ���������������˱������ߵ�Ƶ�ʷֲ�ֱ��ͼ����ͼ�������ߵ�Ƶ�������£�
�������ֽ���������������˱������ߵ�Ƶ�ʷֲ�ֱ��ͼ����ͼ�������ߵ�Ƶ�������£�
���䣨�꣩ |
|
|
|
|
|
|
������ |
|
|
|
|
|
|
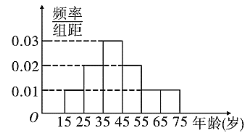
��1������������![]() ��
��![]() �ı��������и����ѡȡ
�ı��������и����ѡȡ![]() �˽��е��飬����ѡȡ��
�˽��е��飬����ѡȡ��![]() ����������
����������![]() �˶���Ȼ���۸�����Ƴ���̬�ȵĸ��ʣ�
�˶���Ȼ���۸�����Ƴ���̬�ȵĸ��ʣ�
��2������������![]() ��
��![]() �ı��������и����ѡȡ
�ı��������и����ѡȡ![]() �˽��е��飬��ѡȡ��
�˽��е��飬��ѡȡ��![]() ���ж���Ȼ���۸�ʵʩ�����Ƴֲ���̬�ȵ�����Ϊ
���ж���Ȼ���۸�ʵʩ�����Ƴֲ���̬�ȵ�����Ϊ![]() �����������
�����������![]() �ķֲ��к���ѧ����.
�ķֲ��к���ѧ����.