题目内容
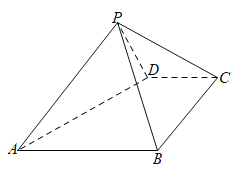
【题目】如图几何体是圆锥的一部分,它是Rt△ABC(及其内部)以一条直角边AB所在直线为旋转轴旋转150°得到的,AB=BC=2,P是弧![]() 上一点,且EB⊥AP.
上一点,且EB⊥AP.
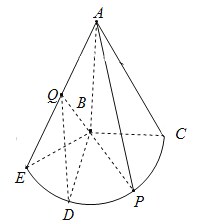
(1)求∠CBP的大小;
(2)若Q为AE的中点,D为弧![]() 的中点,求二面角Q﹣BD﹣P的余弦值;
的中点,求二面角Q﹣BD﹣P的余弦值;
(3)直线AC上是否存在一点M,使得B、D、M、Q四点共面?若存在,请说明点M的位置;若不存在,请说明理由.
【答案】(1)60°(2)![]() (3)存在;直线AC与平面BQD相交,交点为所求点M
(3)存在;直线AC与平面BQD相交,交点为所求点M
【解析】
(1)根据线面垂直推出线线垂直,结合已知角度的大小,即可求得;
(2)根据二面角的定义,作出二面角的补角,求得该补角后,再求出原二面角大小即可.
(3)假设![]() 与平面
与平面![]() 平行,推证矛盾,再说明点
平行,推证矛盾,再说明点![]() 所在位置即为直线与平面的交点即可.
所在位置即为直线与平面的交点即可.
(1)∵AB⊥平面BEC,∴AB⊥BE,
又EB⊥AP,AB∩AP=A,
∴BE⊥平面ABP,则EB⊥BP,
又∠EBC=150°
∴∠CBP=60°;
(2)过Q作QF⊥BE,垂直为F,则QF⊥平面BEC,
过F作FG⊥BD,垂直为G,连接QG,如下图所示:
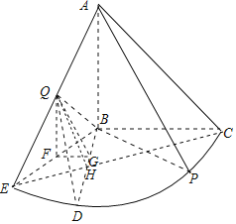
则∠QGF为二面角Q﹣BD﹣E的平面角,
∵D为弧EP的中点,∴∠FBG=45°,
∵Q是AE的中点,∴QF![]() ,
,
因为QF⊥BE,![]() ,故可得
,故可得![]() //
//![]() ,
,
则点![]() 也是
也是![]() 的中点,故BF
的中点,故BF![]()
![]() ,
,
因为QF⊥BE,![]() ,故可得
,故可得![]() //
//![]() ,
,
则点![]() 也是
也是![]() 的中点,故BF
的中点,故BF![]() ,
,
在![]() 中,
中,![]() .
.
因为![]() //
//![]() ,
,![]() 平面
平面![]() ,故可得
,故可得![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,故可得
,故可得![]()
则在![]() 中,
中,
则在Rt△QGF中,可得cos∠QGF![]() ,
,
因为二面角Q﹣BD﹣P的平面角与二面角Q﹣BD﹣E的平面角互补,
∴二面角Q﹣BD﹣P的余弦值为![]() ;
;
(3)直线AC上存在一点M,使得B、D、M、Q四点共面.
事实上,若直线AC与平面BQD相交,则交点为所求点M.
下面说明直线AC与平面BQD相交:
若AC∥平面BQD,
连接EC,交平面BQD于H,
连接QH,则QH∥AC.
∵Q为AE的中点,则H为EC中点,
由∠EBD=45°,∠CBD=105°,
可知H不是EC中点,矛盾.
∴直线AC与平面BQD相交,交点为所求点M.
即直线AC上存在一点M,使得B、D、M、Q四点共面,
该点为直线AC与平面BQD的交点.