题目内容
(本小题满分14分)
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
(Ⅰ) 证明:BC1//平面ACD1;
(Ⅱ)证明:A1D⊥D1E;
(Ⅲ) 当E为AB的中点时,求点E到面 ACD1的距离.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
(Ⅰ) 证明:BC1//平面ACD1;
(Ⅱ)证明:A1D⊥D1E;
(Ⅲ) 当E为AB的中点时,求点E到面 ACD1的距离.
见解析。
(1)证明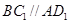 即可.
即可.
(2)证明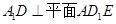 .
.
(3)设点E到面 ACD1的距离为h,然后利用体积法求h即可.具体利用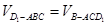 求解.
求解.

Ⅰ)证明:∵AB//A1B1,AB=A1B1,
A1B1// D1C1,A1B1= D1C1,
∴AB// D1C1,AB=D1C1, ……1分
∴AB C1 D1为平行四边形,…… 2分
∴B C1 // AD1, ……3分
又B C1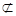 平面ACD1,AD1Ì平面ACD1, ……4分
平面ACD1,AD1Ì平面ACD1, ……4分
所以BC1//平面ACD1. ……5分
(Ⅱ) 证明:∵ AE⊥平面AA1D1D,A1DÌ平面AA1D1D,
∴ A1D⊥AE, ……6分

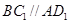 即可.
即可.(2)证明
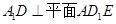 .
.(3)设点E到面 ACD1的距离为h,然后利用体积法求h即可.具体利用
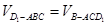 求解.
求解.
Ⅰ)证明:∵AB//A1B1,AB=A1B1,
A1B1// D1C1,A1B1= D1C1,
∴AB// D1C1,AB=D1C1, ……1分
∴AB C1 D1为平行四边形,…… 2分
∴B C1 // AD1, ……3分
又B C1
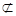 平面ACD1,AD1Ì平面ACD1, ……4分
平面ACD1,AD1Ì平面ACD1, ……4分所以BC1//平面ACD1. ……5分
(Ⅱ) 证明:∵ AE⊥平面AA1D1D,A1DÌ平面AA1D1D,
∴ A1D⊥AE, ……6分


练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
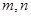 是不同的直线,
是不同的直线,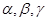 是不同的平面,有以下四个命题:
是不同的平面,有以下四个命题: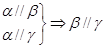 ②
②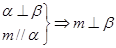 ③
③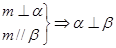 ④
④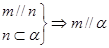
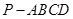 的底面
的底面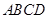 为矩形,且
为矩形,且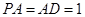 ,
,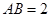 ,
,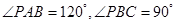 ,(Ⅰ)平面
,(Ⅰ)平面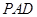 与平面
与平面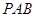 是否垂直?并说明理由;(Ⅱ)求直线
是否垂直?并说明理由;(Ⅱ)求直线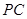 与平面
与平面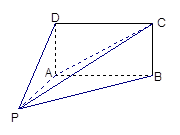
 是两条不同的直线,
是两条不同的直线, 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题: ,
,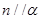 ,则
,则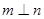 ②若
②若 ,
,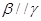 ,
,
 ,
,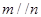 ④若
④若 ,
, ,则
,则
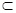 α,要使n⊥β,则应增加的条件是( )
α,要使n⊥β,则应增加的条件是( ) 中,点
中,点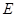 是
是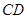 的中点.
的中点. 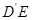 与
与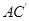 所成的角的余弦值;
所成的角的余弦值;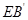 与平面
与平面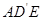 所成的角的余弦值.
所成的角的余弦值.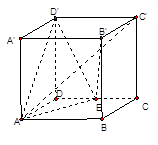
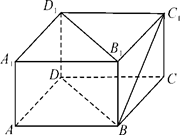
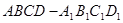 中,二面角
中,二面角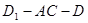 的正切值为
的正切值为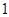
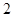
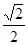
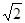 .
.