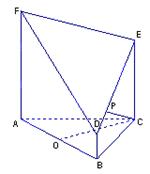
题目内容
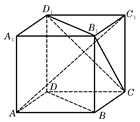
如图,在正方体 中,点
中,点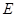 是
是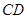 的中点.
的中点.
(1) 求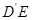 与
与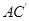 所成的角的余弦值;
所成的角的余弦值;
(2) 求直线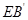 与平面
与平面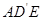 所成的角的余弦值.
所成的角的余弦值.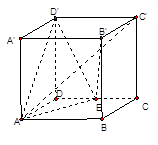
 中,点
中,点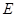 是
是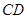 的中点.
的中点. (1) 求
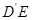 与
与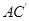 所成的角的余弦值;
所成的角的余弦值;(2) 求直线
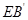 与平面
与平面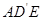 所成的角的余弦值.
所成的角的余弦值.
(1)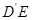 与
与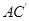 所成的角的余弦值
所成的角的余弦值 .
.
(2)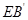 与平面
与平面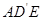 所成的角的余弦值
所成的角的余弦值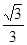 .
.
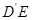 与
与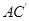 所成的角的余弦值
所成的角的余弦值 .
.(2)
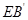 与平面
与平面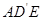 所成的角的余弦值
所成的角的余弦值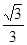 .
. 本题适合用向量法求解。
先建立空间直角坐标系
(1)利用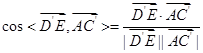 求解.
求解.
(2) )设平面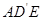 的法向量为
的法向量为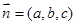 ,求出
,求出 ,然后利用
,然后利用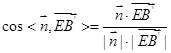 求解即可。
求解即可。
设正方体的棱长为2,分别以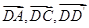 为
为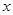 轴、
轴、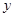 轴
轴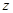 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则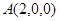
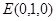
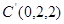
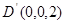 …………………………1分
…………………………1分
(1)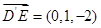 ,
,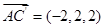 ,故
,故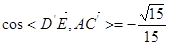 ,………………4分
,………………4分
即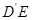 与
与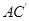 所成的角的余弦值
所成的角的余弦值 .…………………………5分
.…………………………5分
(2)设平面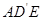 的法向量为
的法向量为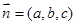 ,
,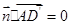 ,
,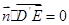 ,则
,则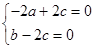 ,
,
令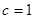 ,则
,则 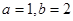 ,∴
,∴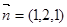 ,
,
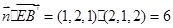 ,
,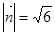 ,
,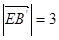 ,∴
,∴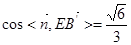 ,
,
故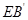 与平面
与平面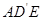 所成的角的余弦值
所成的角的余弦值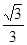 .…………………………………10分
.…………………………………10分
先建立空间直角坐标系
(1)利用
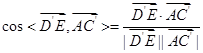 求解.
求解.(2) )设平面
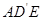 的法向量为
的法向量为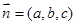 ,求出
,求出 ,然后利用
,然后利用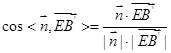 求解即可。
求解即可。设正方体的棱长为2,分别以
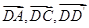 为
为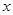 轴、
轴、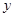 轴
轴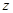 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则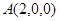
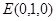
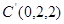
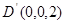 …………………………1分
…………………………1分(1)
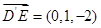 ,
,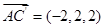 ,故
,故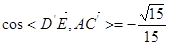 ,………………4分
,………………4分即
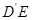 与
与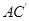 所成的角的余弦值
所成的角的余弦值 .…………………………5分
.…………………………5分(2)设平面
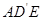 的法向量为
的法向量为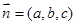 ,
,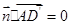 ,
,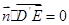 ,则
,则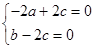 ,
,令
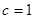 ,则
,则 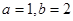 ,∴
,∴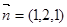 ,
,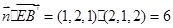 ,
,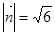 ,
,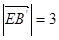 ,∴
,∴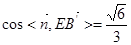 ,
,故
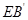 与平面
与平面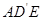 所成的角的余弦值
所成的角的余弦值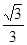 .…………………………………10分
.…………………………………10分
练习册系列答案
相关题目

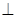 A1D;
A1D;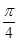 。
。
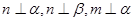
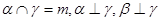
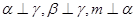
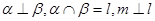
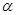 不垂直,那么在平面
不垂直,那么在平面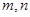 是两条不同的直线,
是两条不同的直线,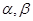 是两个不同的平面,则下列命题中的假命题是
是两个不同的平面,则下列命题中的假命题是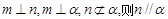
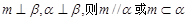
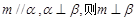
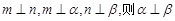
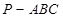 中,
中,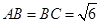 ,平面
,平面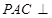 平面
平面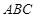 ,
,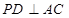 于点
于点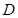 ,
, 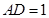 ,
,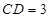 ,
,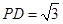 .
.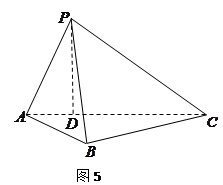
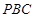 为直角三角形;
为直角三角形;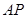 与平面
与平面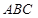 为底面的直棱柱
为底面的直棱柱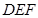 所截而得.
所截而得. 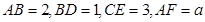 ,
,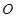 为
为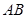 的中点.
的中点.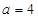 时,求平面
时,求平面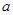 为何值时,在棱
为何值时,在棱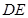 上存在点
上存在点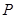 ,使
,使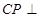 平面
平面