题目内容
在正方体ABCD—A′B′C′D′中，过对角线BD′的一个平面交AA′于E，交CC′于F，则以下结论中错误的是（ ）
| A．四边形BFD′E一定是平行四边形 | B．四边形BFD′E有可能是正方形 |
| C．四边形BFD′E有可能是菱形 | D．四边形BFD′E在底面投影一定是正方形 |
B
解：如图：
①由平面BCB′C′∥平面ADA1D1，并且B、E、F、D′四点共面，
∴ED′∥BF，同理可证，FD′∥EB，故四边形BFD1E一定是平行四边形，故①正确；
②若BFD′E是正方形，有ED′⊥BE，这个与A′D′⊥BE矛盾，故②错误；
③由图得，四边形BFD′E有可能是菱形，故③正确；
④当点E和F分别是对应边的中点时，平面BFD′E⊥平面BB1D′，故④正确．
故答案为B
①由平面BCB′C′∥平面ADA1D1，并且B、E、F、D′四点共面，
∴ED′∥BF，同理可证，FD′∥EB，故四边形BFD1E一定是平行四边形，故①正确；
②若BFD′E是正方形，有ED′⊥BE，这个与A′D′⊥BE矛盾，故②错误；
③由图得，四边形BFD′E有可能是菱形，故③正确；
④当点E和F分别是对应边的中点时，平面BFD′E⊥平面BB1D′，故④正确．
故答案为B
练习册系列答案
阅读快车系列答案
相关题目
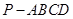中,底面ABCD是边长为1的正方形,
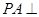平面ABCD,PA=AB,M,N分别为PB,AC的中点,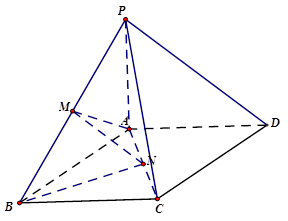 
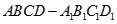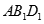中，平面
和平面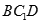
的位置关系为 
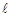与平面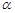
不平行，则（ ）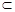
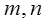和平面
则
的必要非充分条件是
且
且
且
与
成等角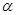
不垂直,那么在平面
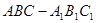的侧棱长与底面边长相等，则
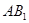与侧面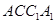
所成角的正弦值等于 .
，
，
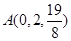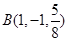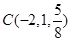是平面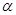
内的三点，设平面
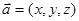，则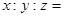
_______________。