Question

【题目】设数列的前项和为，若（），则称是“紧密数列”.

（1）已知数列是“紧密数列”，其前5项依次为，求的取值范围；

（2）若数列的前项和为（），判断是否是“紧密数列”，并说明理由；

（3）设是公比为的等比数列，若与都是“紧密数列”，求的取值范围.

Answer 1

【答案】(1) (2) 是“紧密数列”(3)

【解析】试题分析：

（1）由题意得到关于x的不等式组，求解不等式组可得.

（2）由题意可得．则，结合反比例函数的性质讨论可得，则是“紧密数列”．

（3）由题意， 是“紧密数列”，所以．分类讨论：

①当时数列为“紧密数列”， 满足题意．

②当时，结合等比数列前n项和公式有，对任意恒成立．讨论可得：（ⅰ）当时，满足题意；（ⅱ）当时， 不存在．

则的取值范围是．

试题解析：

（1）由题意得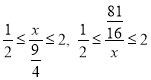： ，所以.

（2）由数列的前项和，

得．

所以， ，

因为对任意， ，即，所以， ，

即是“紧密数列”．

（3）由数列是公比为的等比数列，得，

因为是“紧密数列”，所以．

①当时， ，因为，

所以时，数列为“紧密数列”，故满足题意．

②当时， ，则，因为数列为“紧密数列”，

所以，对任意恒成立．

（ⅰ）当时， ，

即，对任意恒成立．

因为， ， ，

所以， ，

所以，当时， ，对任意恒成立．

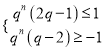（ⅱ）当时， ,即，对任意

恒成立．因为．所以，解得，

又，此时不存在．

综上所述， 的取值范围是．