题目内容
【题目】如图所示,圆O:![]() ,
,![]() ,
,![]() ,D为圆O上任意一点,过D作圆O的切线分别交直线
,D为圆O上任意一点,过D作圆O的切线分别交直线![]() 和
和![]() 于E,F两点,连AF,BE交于点G,若点G形成的轨迹为曲线C.
于E,F两点,连AF,BE交于点G,若点G形成的轨迹为曲线C.
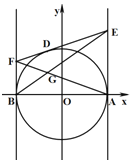
![]() 记AF,BE斜率分别为
记AF,BE斜率分别为![]() ,
,![]() ,求
,求![]() 的值并求曲线C的方程;
的值并求曲线C的方程;
![]() 设直线l:
设直线l:![]() 与曲线C有两个不同的交点P,Q,与直线
与曲线C有两个不同的交点P,Q,与直线![]() 交于点S,与直线
交于点S,与直线![]() 交于点T,求
交于点T,求![]() 的面积与
的面积与![]() 面积的比值
面积的比值![]() 的最大值及取得最大值时m的值.
的最大值及取得最大值时m的值.
【答案】(1) ![]() ,
,![]() (
(![]() ).
).
(2) ![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.
【解析】
分析:(1)先证明![]() ,设
,设![]() ,由
,由![]()
![]()
![]() (
(![]() )故曲线
)故曲线![]() 的方程为
的方程为![]() (
(![]() );(2)由
);(2)由![]() ,利用韦达定理、弦长公式可得
,利用韦达定理、弦长公式可得![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,可得
,可得![]() ,
,![]() ,
,![]() ,
,![]() ,利用换元法结合二次函数配方法可得结果.
,利用换元法结合二次函数配方法可得结果.
详解: (1)设![]() (
(![]() ),
),
易知过![]() 点的切线方程为
点的切线方程为![]() ,其中
,其中![]()
则![]() ,
,![]() ,∴
,∴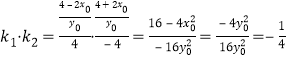
设![]() ,由
,由![]()
![]()
![]() (
(![]() )
)
故曲线![]() 的方程为
的方程为![]() (
(![]() )
)
(2)![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
由![]()
![]() 且
且![]() ,
,![]()
![]()
∵直线![]() 与直线
与直线![]() 交于点
交于点![]() ,与直线
,与直线![]() 交于点
交于点![]()
∴![]() ,
,![]()
∴![]()
∴![]() ,令
,令![]() ,
,![]() 且
且![]()
则![]()
当![]() ,即
,即![]() ,
,![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目