题目内容
【题目】已知椭圆C1： 
=1（a＞b＞0）的左、右焦点分别为F1、F2 ， 其中F2也是抛物线C2：y2=4x的焦点，M是C1与C2在第一象限的交点，且 
（I）求椭圆C1的方程；
（Ⅱ）已知菱形ABCD的顶点A、C在椭圆C1上，顶点B、D在直线7x﹣7y+1=0上，求直线AC的方程．
【答案】解：（I）设点M为（x1 ， y1），∵F2是抛物线y2=4x的焦点，
∴F2（1，0）；
又|MF2|= 
，由抛物线定义知
x1+1= ，即x1= 
；
由M是C1与C2的交点，
∴y12=4x1 ， 即y1=± 
，这里取y1= ；
又点M（ ， ）在C1上，
∴ 
+ 
=1，且b2=a2﹣1，
∴9a4﹣37a2+4=0，∴ 
（舍去），
∴a2=4，b2=3；
∴椭圆C1的方程为： 
（II）∵直线BD的方程为：7x﹣7y+1=0，在菱形ABCD中，AC⊥BD，
不妨设直线AC的方程为x+y=m，
则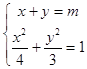 
∴消去y，得7x2﹣8mx+4m2﹣12=0；
∵点A、C在椭圆C1上，
∴（﹣8m）2﹣4×7×（4m2﹣12）＞0，即m2＜7，∴﹣ 
＜m＜ ；
设A（x1 ， y1），C（x2 ， y2），
则x1+x2= 
，y1+y2=（﹣x1+m）+（﹣x2+m）=﹣（x1+x2）+2m=﹣ +2m= 
，
∴AC的中点坐标为 
，
由菱形ABCD知，点 也在直线BD：7x﹣7y+1=0上，
即7× 
﹣7× 
+1=0，∴m=﹣1，由m=﹣1∈ 
知：
直线AC的方程为：x+y=﹣1，即x+y+1=0
【解析】（Ⅰ）设点M为（x1 ， y1），由F2是抛物线y2=4x的焦点，知F2（1，0）；|MF2|= 
，由抛物线定义知x1+1= ，即x1= 
；由M是C1与C2的交点，y12=4x1 ， 由此能求出椭圆C1的方程．（Ⅱ）直线BD的方程为：7x﹣7y+1=0，在菱形ABCD中，AC⊥BD，设直线AC的方程为x+y=m，由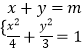 
，得7x2﹣8mx+4m2﹣12=0．由点A、C在椭圆C1上，知（﹣8m）2﹣4×7×（4m2﹣12）＞0，由此能导出直线AC的方程．
