题目内容
【题目】已知a＞0，b＞0，函数f（x）=|x+a|+|2x﹣b|的最小值为1．
（1）求证：2a+b=2；
（2）若a+2b≥tab恒成立，求实数t的最大值．
【答案】
（1）解：法一：f（x）=|x+a|+|2x﹣b|=|x+a|+|x﹣ 
|+|x﹣ |，
∵|x+a|+|x﹣ |≥|（x+a）﹣（x﹣ ）|=a+ 且|x﹣ |≥0，
∴f（x）≥a+ ，当x= 时取等号，即f（x）的最小值为a+ ，
∴a+ =1，2a+b=2；
法二：∵﹣a＜ ，∴f（x）=|x+a|+|2x﹣b|=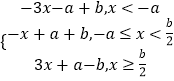 
，
显然f（x）在（﹣∞， ]上单调递减，f（x）在[ ，+∞）上单调递增，
∴f（x）的最小值为f（ ）=a+ ，
∴a+ =1，2a+b=2
（2）解：方法一：∵a+2b≥tab恒成立，∴ 
≥t恒成立，
= 
+ 
=（ + ）（2a+b ） 
= （1+4+ 
+ 
） 
，
当a=b= 
时， 取得最小值 
，
∴ ≥t，即实数t的最大值为 ；
方法二：∵a+2b≥tab恒成立，
∴ ≥t恒成立，
t≤ = + 恒成立，
+ = + 
≥ 
= ，
∴ ≥t，即实数t的最大值为 ；
方法三：∵a+2b≥tab恒成立，
∴a+2（2﹣a）≥ta（2﹣a）恒成立，
∴2ta2﹣（3+2t）a+4≥0恒成立，
∴（3+2t）2﹣326≤0，
∴ ≤t≤ ，实数t的最大值为
【解析】（1）法一：根据绝对值的性质求出f（x）的最小值，得到x= 时取等号，证明结论即可；法二：根据f（x）的分段函数的形式，求出f（x）的最小值，证明即可；（2）法一，二：问题转化为 ≥t恒成立，根据基本不等式的性质求出 的最小值，从而求出t的范围即可；法三：根据二次函数的性质判断即可．
