题目内容
(本小题满分12分)
某建筑物的上半部分是多面体 , 下半部分是长方体
, 下半部分是长方体 (如图). 该建筑物的正视图和侧视图(如图), 其中正(主)视图由正方形和等腰梯形组合而成,侧(左)视图由长方形和等腰三角形组合而成.
(如图). 该建筑物的正视图和侧视图(如图), 其中正(主)视图由正方形和等腰梯形组合而成,侧(左)视图由长方形和等腰三角形组合而成.


(Ⅰ)求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(Ⅱ)求二面角 的余弦值;
的余弦值;
(Ⅲ)求该建筑物的体积.
某建筑物的上半部分是多面体
 , 下半部分是长方体
, 下半部分是长方体 (如图). 该建筑物的正视图和侧视图(如图), 其中正(主)视图由正方形和等腰梯形组合而成,侧(左)视图由长方形和等腰三角形组合而成.
(如图). 该建筑物的正视图和侧视图(如图), 其中正(主)视图由正方形和等腰梯形组合而成,侧(左)视图由长方形和等腰三角形组合而成.

(Ⅰ)求直线
 与平面
与平面 所成角的正弦值;
所成角的正弦值;(Ⅱ)求二面角
 的余弦值;
的余弦值;(Ⅲ)求该建筑物的体积.
(1)直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 .
.
(2)二面角 的余弦值为
的余弦值为 .(3)建筑物的体积为
.(3)建筑物的体积为 .
.
 与平面
与平面 所成角的正弦值为
所成角的正弦值为 .
.(2)二面角
 的余弦值为
的余弦值为 .(3)建筑物的体积为
.(3)建筑物的体积为 .
.试题分析:解法1:(1)作
 平面
平面 ,
,垂足为
 ,连接
,连接 ,则
,则 是直线
是直线 与平面
与平面 所成的角. ………………1分
所成的角. ………………1分由于平面

 平面
平面 ,
,故
 是直线
是直线 与平面
与平面 所成的角.……2分
所成的角.……2分作
 ,垂足为
,垂足为 ,连接
,连接 ,
,∵
 平面
平面 ,∴
,∴ .
.∵
 平面
平面 ,
, 平面
平面 ,
,∴
 平面
平面 .
.由题意知

 ,
,在Rt△
 中,
中, ,
,在Rt△
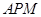 中,
中, ,在Rt△
,在Rt△ 中,
中, ,
,∴直线
 与平面
与平面 所成角的正弦值为
所成角的正弦值为 . ………………………… 4分
. ………………………… 4分(2)延长
 交
交 于点
于点 ,连接
,连接 ,由(1)知
,由(1)知 平面
平面
∵
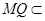 平面
平面 ,∴
,∴
 .∵
.∵ ,∴
,∴ .
. ∴
 是二面角
是二面角 的平面角. ………………………… 6分
的平面角. ………………………… 6分在△
 中,
中, ,∵
,∵ ,∴
,∴ .
.∴二面角
 的余弦值为
的余弦值为 . …………………………… 8分
. …………………………… 8分(3)作
 交
交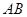 于点
于点 ,作
,作 交
交 于点
于点 ,由题意知多面体
,由题意知多面体 可分割为两个等体积的四棱锥
可分割为两个等体积的四棱锥 和
和 和一个直三棱柱
和一个直三棱柱 .
.四棱锥
 的体积为
的体积为
 ,
, 直三棱柱
 的体积为
的体积为 ,
, ∴多面体
 的体积为
的体积为
 . ……………10分
. ……………10分长方体
 的体积为
的体积为 . ………… 11分
. ………… 11分∴建筑物的体积为
 . …………………… 12分
. …………………… 12分解法2:(参照解法1评分)
(1)以点
 为原点,
为原点, 所在直线为
所在直线为 轴,
轴, 所在直线为
所在直线为 轴,
轴, 所在直线为
所在直线为 轴,建立空间直角坐标系
轴,建立空间直角坐标系 (如图),
(如图),
作
 平面
平面 ,垂足为
,垂足为 ,作
,作 ,垂足为
,垂足为 ,依题意知
,依题意知 ,
, ,
,则

 ,
, .
.∴
 .
.∵
 平面
平面 ,∴平面
,∴平面 的一个法向量为
的一个法向量为 .
.设直线
 与平面
与平面 所成角为
所成角为 ,则
,则

 .
. ∴直线
 与平面
与平面 所成角的正弦值为
所成角的正弦值为 .
.(2)由(1)知
 ,设平面
,设平面 的法向量为
的法向量为
 ,
,由
 ,
, 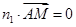 ,得
,得 取平面
取平面 的一个法向量为
的一个法向量为
 .
.设平面
 的法向量为
的法向量为
 ,由
,由 ,
, ,得
,得
∴平面
 的一个法向量为
的一个法向量为
 .
.∵



 , ∴二面角
, ∴二面角 的余弦值为
的余弦值为 .
.(3)(同解法1) 略
点评:本题通过考查直线与直线,直线与平面、平面与平面的位置关系等基础知识,考查空间想像能力、推理论证能力、运算求解能力、考查化归与转化思想,函数与方程思想等.利用空间向量,往往使问题的解答得以简化,属中档题。

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 内有一个三棱柱
内有一个三棱柱 ,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径.
,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径.
 平面
平面 ;
; ,在圆柱
,在圆柱 .
. 与平面
与平面 所成的角为
所成的角为 ,当
,当 的值.
的值.

 的各条棱长都相等,
的各条棱长都相等, 是侧棱
是侧棱 的中点,则异面直线
的中点,则异面直线 所成的角的大小是
所成的角的大小是 

 中
中 ,
, 平面
平面 ,
,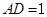 ,
, ,
, .
.

 ;
; 与平面
与平面 所成的角;
所成的角; 在棱
在棱 ,若
,若 ∥平面
∥平面 ,求
,求 的值.
的值.








 是正三角形ABC的斜二测画法的水平放置直观图,若
是正三角形ABC的斜二测画法的水平放置直观图,若 ,那么
,那么 的面积为 .
的面积为 .