题目内容
(本题满分12分)如图,在底面为直角梯形的四棱锥 中
中 ,
, 平面
平面 ,
,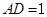 ,
, ,
, .
.

(Ⅰ)求证:
 ;
;
(Ⅱ)求直线 与平面
与平面 所成的角;
所成的角;
(Ⅲ)设点 在棱
在棱 上,
上, ,若
,若 ∥平面
∥平面 ,求
,求 的值.
的值.
 中
中 ,
, 平面
平面 ,
,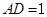 ,
, ,
, .
.
(Ⅰ)求证:

 ;
;(Ⅱ)求直线
 与平面
与平面 所成的角;
所成的角;(Ⅲ)设点
 在棱
在棱 上,
上, ,若
,若 ∥平面
∥平面 ,求
,求 的值.
的值.(Ⅰ)先根据 证明
证明 ,再证明
,再证明 从而得证。
从而得证。
(Ⅱ)
(Ⅲ)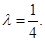
 证明
证明 ,再证明
,再证明 从而得证。
从而得证。(Ⅱ)

(Ⅲ)
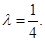
【方法一】(1)证明:由题意知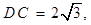 则
则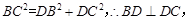
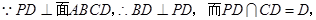
 (4分)
(4分)
(2)∵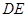 ∥
∥ ,又
,又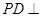 平面
平面 .
.
∴平面
 平面
平面 .过
.过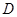 作
作 //
// 交
交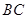 于
于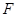 过点
过点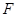 作
作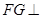
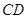 交
交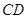 于
于 ,则∠
,则∠ 为直线
为直线 与平面
与平面 所成的角. 在Rt△
所成的角. 在Rt△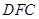 中,∠
中,∠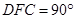 ,
,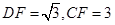
∴ ,∴∠
,∴∠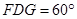 .即直线
.即直线 与平面
与平面 所成角为
所成角为 (8分)
(8分)
(3)连结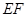 ,∵
,∵ ∥
∥ ,
,
∴ ∥平面
∥平面 .
.
又∵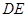 ∥平面
∥平面 ,
,
∴平面 ∥平面
∥平面 ,∴
,∴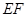 ∥
∥ .
.
又∵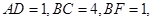
∴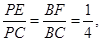 ∴
∴ ,即
,即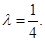 (12分)
(12分)
【方法二】如图,在平面ABCD内过D作直线DF//AB,交BC于F,分别以DA、DF、DP所在的直线为x、y、z轴建立空间直角坐标系.

(1)设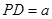 ,则
,则 ,
,
∵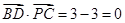 ,∴
,∴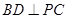 (4分)
(4分)
(2)由(1)知 .
.
由条件知A(1,0,0),B(1,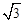 ,0),
,0),
 .设
.设
则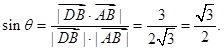
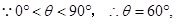
即直线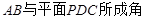 为
为 . (8分)
. (8分)
(3)由(2)知C(-3,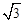 ,0),记P(0,0,a),则
,0),记P(0,0,a),则
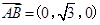 ,
,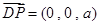 ,
,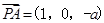 ,
,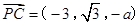 ,
,
而 ,所以
,所以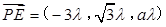 ,
,

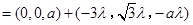 =
=
设 为平面PAB的法向量,则
为平面PAB的法向量,则 ,即
,即 ,即
,即 .
.
 进而得
进而得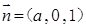 ,
,
由 ,得
,得 ∴
∴
 (12分)
(12分)
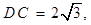 则
则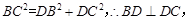
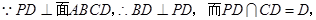
 (4分)
(4分)(2)∵
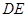 ∥
∥ ,又
,又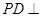 平面
平面 .
.∴平面

 平面
平面 .过
.过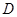 作
作 //
// 交
交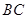 于
于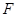 过点
过点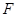 作
作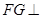
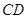 交
交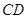 于
于 ,则∠
,则∠ 为直线
为直线 与平面
与平面 所成的角. 在Rt△
所成的角. 在Rt△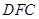 中,∠
中,∠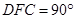 ,
,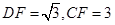
∴
 ,∴∠
,∴∠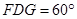 .即直线
.即直线 与平面
与平面 所成角为
所成角为 (8分)
(8分)(3)连结
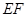 ,∵
,∵ ∥
∥ ,
,∴
 ∥平面
∥平面 .
.又∵
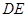 ∥平面
∥平面 ,
,∴平面
 ∥平面
∥平面 ,∴
,∴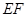 ∥
∥ .
.又∵
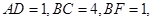
∴
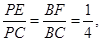 ∴
∴ ,即
,即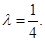 (12分)
(12分)【方法二】如图,在平面ABCD内过D作直线DF//AB,交BC于F,分别以DA、DF、DP所在的直线为x、y、z轴建立空间直角坐标系.

(1)设
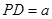 ,则
,则 ,
,∵
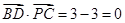 ,∴
,∴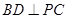 (4分)
(4分)(2)由(1)知
 .
.由条件知A(1,0,0),B(1,
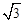 ,0),
,0), .设
.设
则
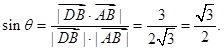
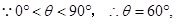
即直线
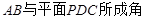 为
为 . (8分)
. (8分)(3)由(2)知C(-3,
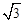 ,0),记P(0,0,a),则
,0),记P(0,0,a),则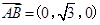 ,
,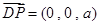 ,
,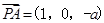 ,
,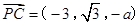 ,
,而
 ,所以
,所以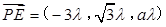 ,
,
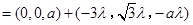 =
=
设
 为平面PAB的法向量,则
为平面PAB的法向量,则 ,即
,即 ,即
,即 .
. 进而得
进而得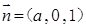 ,
,由
 ,得
,得 ∴
∴
 (12分)
(12分)
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,顶点都在一个球面上.若该球的表面积为
,顶点都在一个球面上.若该球的表面积为 ,则棱长
,则棱长 ___________.
___________.  ,且
,且 是垂足,
是垂足,


 ,则
,则 ( )
( )




 , 下半部分是长方体
, 下半部分是长方体 (如图). 该建筑物的正视图和侧视图(如图), 其中正(主)视图由正方形和等腰梯形组合而成,侧(左)视图由长方形和等腰三角形组合而成.
(如图). 该建筑物的正视图和侧视图(如图), 其中正(主)视图由正方形和等腰梯形组合而成,侧(左)视图由长方形和等腰三角形组合而成.

 与平面
与平面 所成角的正弦值;
所成角的正弦值; 的余弦值;
的余弦值;
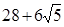



 中,
中, ,则从
,则从 点沿表面到
点沿表面到 点的最短距离为 .
点的最短距离为 .