题目内容
2.已知抛物线y2=2x上有两点P(x1,y1)、Q(x2,y2),过PQ的中点M作x轴的平行线,交抛物线于R点,求证:S△PQR=$\frac{1}{16}$|y1-y2|3.分析 过P,Q,R三点向准线引垂线,垂足分别为A,B,C,则S△PQR=SABQP-SACRP-SBCRQ,结合梯形面积公式,可得结论.
解答 证明:∵抛物线y2=2x的焦点($\frac{1}{2}$,0),准线x=-$\frac{1}{2}$,
过P,Q,R三点向准线引垂线,垂足分别为A,B,C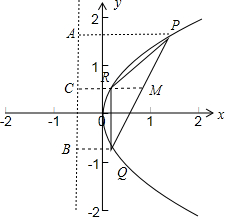
∵P(x1,y1)、Q(x2,y2),即P($\frac{1}{2}$y12,y1),Q($\frac{1}{2}$y22,y2),
∴M点坐标为:($\frac{{x}_{1}{+x}_{2}}{2}$,$\frac{{y}_{1}{+y}_{2}}{2}$),R坐标为:($\frac{{(y}_{1}{+y}_{2})^{2}}{8}$,$\frac{{y}_{1}{+y}_{2}}{2}$),
A点坐标为:(-$\frac{1}{2}$,y1),B点坐标为(-$\frac{1}{2}$,y2),C点坐标为:(-$\frac{1}{2}$,$\frac{{y}_{1}{+y}_{2}}{2}$),
S△PQR=SABQP-SACRP-SBCRQ
=$\frac{1}{2}$[($\frac{1}{2}$y12+$\frac{1}{2}$)+($\frac{1}{2}$y22+$\frac{1}{2}$)]•|y1-y2|-$\frac{1}{2}$[($\frac{1}{2}$y12+$\frac{1}{2}$)+($\frac{{(y}_{1}{+y}_{2})^{2}}{8}$+$\frac{1}{2}$)]•$\frac{1}{2}$|y1-y2|-$\frac{1}{2}$[($\frac{{(y}_{1}{+y}_{2})^{2}}{8}$+$\frac{1}{2}$)+($\frac{1}{2}$y22+$\frac{1}{2}$)]•$\frac{1}{2}$|y1-y2|
=$\frac{1}{16}$|y1-y2|3.
点评 本题考查的知识点是抛物线的简单性质,三角形面积公式与梯形面积公式,难度中档.

| A. | 2$\sqrt{3}$ | B. | $\frac{5}{2}$$\sqrt{6}$ | C. | 3$\sqrt{6}$ | D. | $\frac{7\sqrt{7}}{2}$ |
| A. | (-1,+∞) | B. | (-1,1) | C. | [-1,+∞) | D. | [-1,1) |
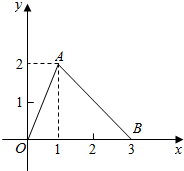 函数f(x)的图象是如图所示的折线段OAB,点A的坐标为(1,2),点B的坐标为(3,0),定义函数g(x)=f(x)(1-x).
函数f(x)的图象是如图所示的折线段OAB,点A的坐标为(1,2),点B的坐标为(3,0),定义函数g(x)=f(x)(1-x).