题目内容
18.海面上有两座灯塔A,B,与观察站C的距离都是m km,灯塔A在观察站C的北偏东40°,灯塔B在观察站C的南偏东20°,则灯塔A,B间的距离是( )| A. | m km | B. | $\sqrt{2}m\\;km$ km | C. | 2m km | D. | $\sqrt{3}m$ km |
分析 先根据题意求得∠ACB,进而根据余弦定理求得AB
解答 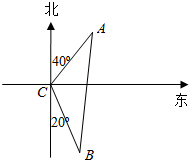 解:依题意知∠ACB=180°-20°-40°=120°,
解:依题意知∠ACB=180°-20°-40°=120°,
在△ABC中,由余弦定理知AB2=AC2+BC2-2AC•BCcos∠ACB=m2+m2-2m2cos120°=3m2,
即灯塔A与灯塔B的距离为$\sqrt{3}$mkm.
故选:D.
点评 本题给出实际应用问题,求海洋上灯塔A与灯塔B的距离.着重考查了三角形内角和定理和运用余弦定理解三角形等知识,属于基础题.

练习册系列答案
相关题目
8.若命题P:?x0$>0,{x}_{0}^{2}$+2x0+3≤0,则命题P的否定¬P是( )
| A. | ?x>0,x2+2x+3>0 | B. | ?x>0,x2+2x+3≥0 | C. | ?x≤0,x2+2x+3<0 | D. | ?x≤0,x2+2x+3≤0 |
13.设点M(-1,$\sqrt{3}$)是抛物线y2=2px(p>0)准线上-点,过该抛物线焦点F的直线过A、B两点,若 $\overrightarrow{FM}$•$\overrightarrow{FA}$=0,则△MAB的面积为 ( )
| A. | 2$\sqrt{3}$ | B. | $\frac{5}{2}$$\sqrt{6}$ | C. | 3$\sqrt{6}$ | D. | $\frac{7\sqrt{7}}{2}$ |
10.意义运算“*”如下:x*y=$\left\{\begin{array}{l}{x,x≥y}\\{y,x<y}\end{array}\right.$,若函数f(x)=(1-2x)*(2x-3)+m的图象与x轴有两个交点,则实数m的取值范围是( )
| A. | (-1,+∞) | B. | (-1,1) | C. | [-1,+∞) | D. | [-1,1) |
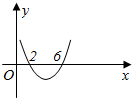 已知函数f(x)=ax(x-c)2在点x=x0处取得极大值32,其导函数y=f′(x)的图象经过点(2,0)、(6,0),如图.
已知函数f(x)=ax(x-c)2在点x=x0处取得极大值32,其导函数y=f′(x)的图象经过点(2,0)、(6,0),如图.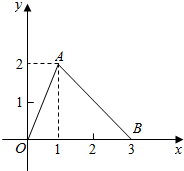 函数f(x)的图象是如图所示的折线段OAB,点A的坐标为(1,2),点B的坐标为(3,0),定义函数g(x)=f(x)(1-x).
函数f(x)的图象是如图所示的折线段OAB,点A的坐标为(1,2),点B的坐标为(3,0),定义函数g(x)=f(x)(1-x).