题目内容
函数f(x)=ax2+(a-3)x+1在区间[-1,+∞)上是递减的,则实数a的取值范围是( )
(A)[-3,0) (B)(-∞,-3]
(C)[-2,0] (D)[-3,0]
D
【解析】当a=0时,f(x)=-3x+1显然成立,
当a≠0时,需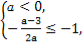
解得-3≤a<0,
综上可得-3≤a≤0.
【误区警示】本题易忽视a=0这一情况而误选A,失误的原因是将关于x的函数误认为是二次函数.
练习册系列答案
相关题目
题目内容
函数f(x)=ax2+(a-3)x+1在区间[-1,+∞)上是递减的,则实数a的取值范围是( )
(A)[-3,0) (B)(-∞,-3]
(C)[-2,0] (D)[-3,0]
D
【解析】当a=0时,f(x)=-3x+1显然成立,
当a≠0时,需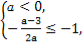解得-3≤a<0,
综上可得-3≤a≤0.
【误区警示】本题易忽视a=0这一情况而误选A,失误的原因是将关于x的函数误认为是二次函数.
