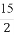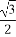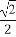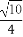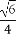Question

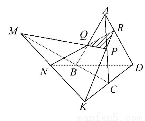
如图,A,B,C,D为空间四点.在△ABC中,AB=2,AC=BC=.等边三角形ADB以AB为轴转动.

(1)当平面ADB⊥平面ABC时,求CD.

(2)当△ADB转动时,是否总有AB⊥CD?证明你的结论.

 

Answer 1

(1)2 (2)见解析

【解析】(1)取AB的中点E,

连接DE,CE,

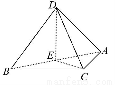
因为△ADB是等边三角形,

所以DE⊥AB.

当平面ADB⊥平面ABC时,

因为平面ADB∩平面ABC=AB,

所以DE⊥平面ABC,可知DE⊥CE.

由已知可得DE=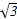,EC=1,

在Rt△DEC中,CD=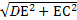=2.

(2)当△ADB以AB为轴转动时,总有AB⊥CD.

证明:

①当D在平面ABC内时,

因为AC=BC,AD=BD,

所以C,D都在线段AB的垂直平分线上,即AB⊥CD.

②当D不在平面ABC内时,

由(1)知AB⊥DE.

又因AC=BC,所以AB⊥CE.

又DE,CE为相交直线,所以AB⊥平面CDE.

由CD?平面CDE,得AB⊥CD.

综上所述,总有AB⊥CD.